Parametric Curves: Example 2: Unit Circle

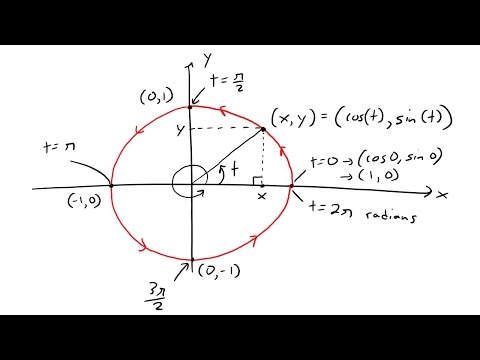
In this video I go over another example on parametric curves and this time graph the curve formed by the parametric equations x = cos(t) and y = sin(t). Using the Pythagorean trig identity, sin^2(x) + cos^2(x) = 1, I show that in fact the curve defined by these parametric equations is a unit circle, which is a circle with a radius of 1. The circle is formed by starting at the point (1, 0) and then rotating around counterclockwise one full rotation. The parameter t, in this specific example represents the angle that is formed from the origin to a point on the unit circle. This is a very interesting video on how parametric equations define common shapes and curves that we are accustomed to, such as a circle. So make sure to watch this video!

Download the notes in my video:

Related Videos:

------------------------------------------------------

[mes]

I don't always go over parametric equations but when I do I usually show how they can be used to graph common curves such as a circle ;)


#GetOnSteem

[SOBIESKI_freedom]

Great stuff. Kudos!

Will you eventually be showing us the parametric equations for superellipses (of which circles are a subset)?