filmov
tv
70.(1+e^x/y)dx+e^x/y(1-x/y)dy=0
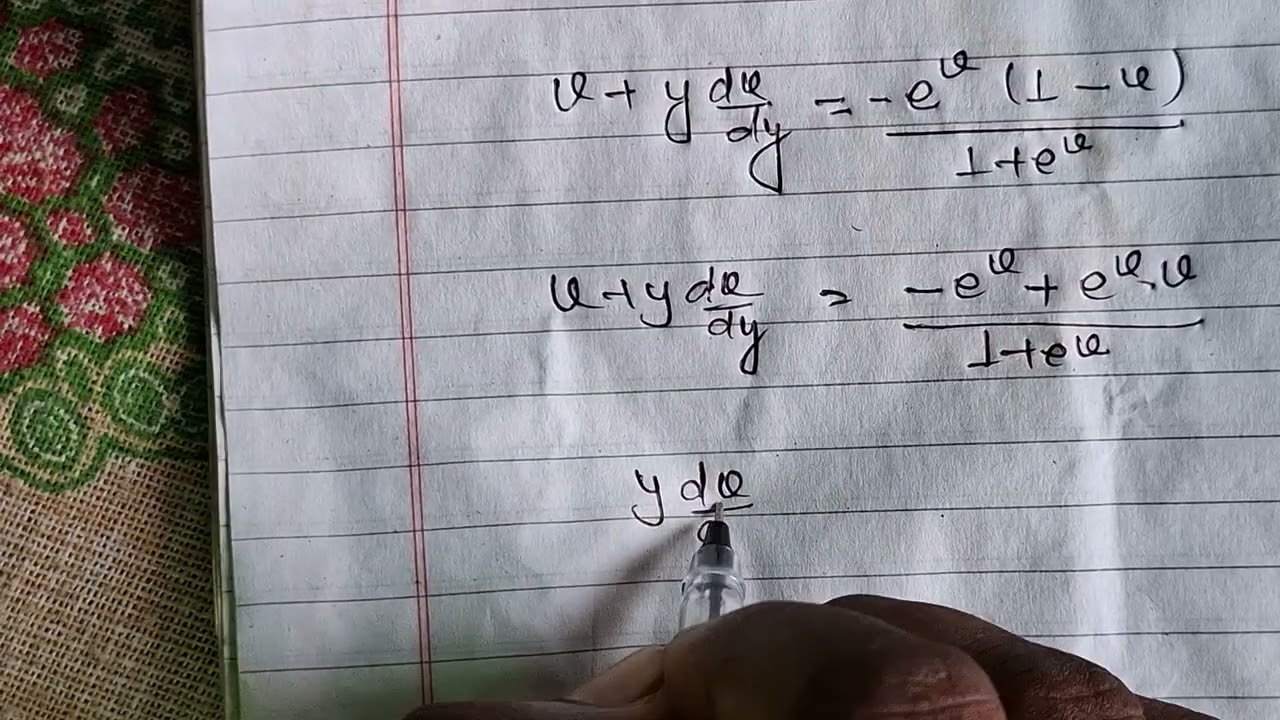
Показать описание
#solvehomogeneousdifferentialequation #equationofthefirstorderandthefirstdegree #maths #variableseparable
A differential equation of the form f(x,y)dy = g(x,y)dx is said to be homogeneous differential equation if the degree of f(x,y) and g(x, y) is same. A function of form F(x,y) which can be written in the form kn F(x,y) is said to be a homogeneous function of degree n, for k≠0. Hence, f and g are the homogeneous functions of the same degree of x and y. Here, the change of variable y = ux directs to an equation of the form;
dx/x = h(u) du
which could be easily integrated.
Contrarily, a differential equation is homogeneous if it is a similar function of the anonymous function and its derivatives. For linear differential equations, there are no constant terms. The solutions of any linear ordinary differential equation of any degree or order may be calculated by integration from the solution of the homogeneous equation achieved by eliminating the constant term.
Steps to Solve Homogeneous Differential Equation
You must have learned to solve the differential equations in previous sections. To solve a homogeneous differential equation following steps are followed:-
Given differential equation of the type
Step 1- Substitute y = vx in the given differential equation.
Step 2 – Differentiating, we get,
Now substitute the value of and y in the given differential equation, we get
Step 3 – Separating the variables, we get
Step 4 – Integrating both side of equation, we have
Step 5 – After integration we replace v=y/x
A differential equation of the form f(x,y)dy = g(x,y)dx is said to be homogeneous differential equation if the degree of f(x,y) and g(x, y) is same. A function of form F(x,y) which can be written in the form kn F(x,y) is said to be a homogeneous function of degree n, for k≠0. Hence, f and g are the homogeneous functions of the same degree of x and y. Here, the change of variable y = ux directs to an equation of the form;
dx/x = h(u) du
which could be easily integrated.
Contrarily, a differential equation is homogeneous if it is a similar function of the anonymous function and its derivatives. For linear differential equations, there are no constant terms. The solutions of any linear ordinary differential equation of any degree or order may be calculated by integration from the solution of the homogeneous equation achieved by eliminating the constant term.
Steps to Solve Homogeneous Differential Equation
You must have learned to solve the differential equations in previous sections. To solve a homogeneous differential equation following steps are followed:-
Given differential equation of the type
Step 1- Substitute y = vx in the given differential equation.
Step 2 – Differentiating, we get,
Now substitute the value of and y in the given differential equation, we get
Step 3 – Separating the variables, we get
Step 4 – Integrating both side of equation, we have
Step 5 – After integration we replace v=y/x
 0:04:16
0:04:16
 0:00:34
0:00:34
 0:01:43
0:01:43
 0:04:47
0:04:47
 0:00:15
0:00:15
 0:00:14
0:00:14
 0:01:51
0:01:51
 0:00:11
0:00:11
 0:00:23
0:00:23
 0:02:45
0:02:45
 0:00:22
0:00:22
 0:00:32
0:00:32
 0:03:08
0:03:08
 0:00:25
0:00:25
 0:00:57
0:00:57
 0:17:40
0:17:40
 0:00:12
0:00:12
 0:00:47
0:00:47
 0:00:20
0:00:20
 0:04:16
0:04:16
 0:00:15
0:00:15
 0:01:48
0:01:48
 0:07:39
0:07:39
 0:00:13
0:00:13