filmov
tv
This Integral is Nuts

Показать описание
Can you solve this seemingly simple Integral of x integrated with respect to x²? Let's cover the Riemann-Stieltjes Integral, shall we? :) Enjoy! =D
Help me create more free content! =)
0:00 Intro
1:25 Riemann Integral
7:43 Stieltjes Integral
17:31 The Cool Way
This Integral is Nuts
I Computed An Integral That Breaks Math
This integral looks crazy
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Volle Kontrolle bei Stromausfall: USV Integration mit Home Assistant! [NUT]
Looking Impossible Integration solved!
Challenge 31: Can You Evaluate This Crazy Integral?!!
Feynman Integral - I can’t believe I got it right!! #integrationtricks #calculus #mathchallenge
CRAZY integral from MIT (integrating in N dimensions as N goes to infinity?)
Can you solve this integral equation?
This famous integral is perfect for Feynman's integration technique
One crazy looking integral
A wonderfully crazy integral
MIT Integration Bee Qualifier!
Solving Gaussian Integral in Seconds
integral gaussiana (gaussian integral)
Feynman's trick to avoid integration by parts
INSANE integral solved using Feynman's technique
A crazy yet perfect integral
MIT Integration Bee Qualifier Solved In 30 Seconds
INTEGRATION IMPORTANT QUESTION | CBSE BOARDS | CLASS 12 MATHS | STATE BOARDS | CUET #shorts_
This integral is speaking VOLUMES! Doing the triple Gaussian using spherical and polar coordinates
Can you solve this crazy integral ?
Crazy Trig Integral: Symmetry and Substitution
Комментарии
 0:23:03
0:23:03
 0:04:20
0:04:20
 0:16:14
0:16:14
 0:00:09
0:00:09
 0:22:10
0:22:10
 0:00:55
0:00:55
 0:01:26
0:01:26
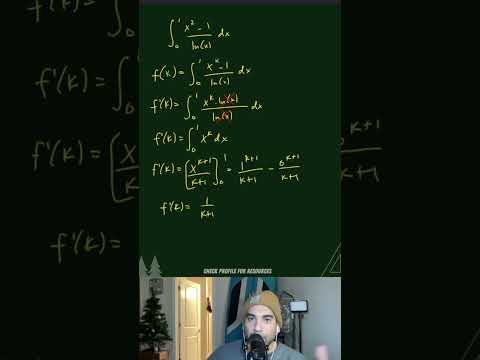 0:01:01
0:01:01
 0:08:47
0:08:47
 0:00:43
0:00:43
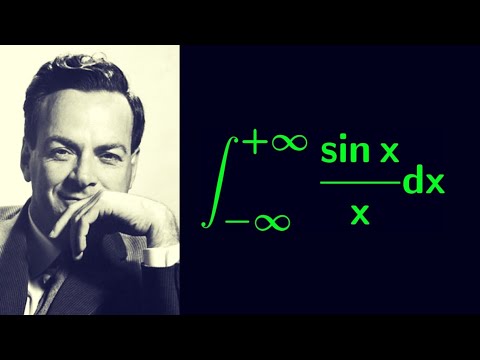 0:10:57
0:10:57
 0:13:06
0:13:06
 0:08:02
0:08:02
 0:00:35
0:00:35
 0:00:25
0:00:25
 0:00:20
0:00:20
 0:00:44
0:00:44
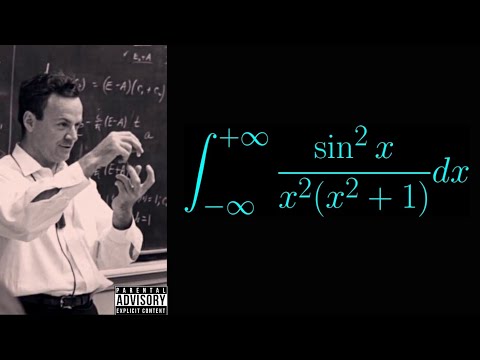 0:14:47
0:14:47
 0:12:24
0:12:24
 0:00:19
0:00:19
 0:00:33
0:00:33
 0:13:00
0:13:00
 0:07:44
0:07:44
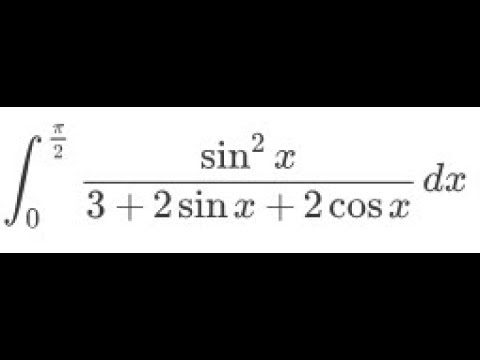 0:09:22
0:09:22