filmov
tv
How to calculate the sum of interior angles of a hexagon

Показать описание
In this clip learn how to calculate the sum of interior angles of a hexagon.
To calculate the sum of the interior angles the following formula is used ((n-2)180)/n.
Regular polygon are 2D shapes where all of the sides are congruent and the measure of each angle is congruent.
These polygons are also known as equilateral and equiangular.
✅Recommended tutorials:
📐 How to calculate sum of interior angles of a octagon
📒Recommended playlists:
📐 Geometry Tutorials
📐 How to calculate interior angles
📐 How to calculate exterior angles
-------------------------------------------------
FOLLOW ME:
--------------------------------------------
Disclaimer: This is not a sponsored video.
#spellermathtutorials #iylili #geometry #mathgoals2019 #interior #angles #polygons #regular #practicemakesprogress #learnsomethingnewcrew
To calculate the sum of the interior angles the following formula is used ((n-2)180)/n.
Regular polygon are 2D shapes where all of the sides are congruent and the measure of each angle is congruent.
These polygons are also known as equilateral and equiangular.
✅Recommended tutorials:
📐 How to calculate sum of interior angles of a octagon
📒Recommended playlists:
📐 Geometry Tutorials
📐 How to calculate interior angles
📐 How to calculate exterior angles
-------------------------------------------------
FOLLOW ME:
--------------------------------------------
Disclaimer: This is not a sponsored video.
#spellermathtutorials #iylili #geometry #mathgoals2019 #interior #angles #polygons #regular #practicemakesprogress #learnsomethingnewcrew
How to use the SUM function in Microsoft Excel
How to Make a Totaling Column Formula in Excel : Using Microsoft Excel
How To Find The Sum of an Arithmetic Series - Algebra
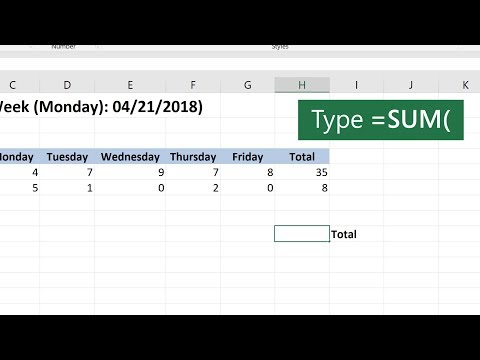
How to Sum a Column or Row of Excel Cells
Add numbers in columns in a Word table: Insert formula to sum a column or row of table in Word?
How to Sum a Column in Excel
Summation Formulas and Sigma Notation - Calculus
Finding the sum or an arithmetic series using summation notation
GRADE 11/12 - CALCULATING THE SUM OF DIGITS
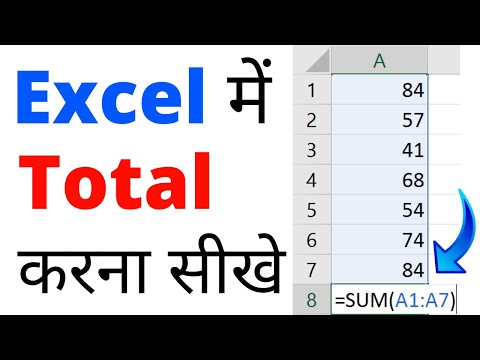
excel me total kaise kare | How to calculate total in excel (Easy Way)
Excel SUM and SUMIF Formula in Excel
The Power Of SUM and AVERAGE In Excel
How to calculate in word table (sum, multiplication, average)
How to Use the Sum Function in Google Sheets
How to sum by month
ANOVA 1: Calculating SST (total sum of squares) | Probability and Statistics | Khan Academy
How to find the sum of a mixed number and a fraction
How to Calculate Running Totals or Cumulative Sum for a Range of Cells in Excel 2016
How to Calculate SUM of Every Alternative Cells in Excel
How to Sum an Entire Column or Row in Excel
Combine duplicate rows and sum the values in Excel (Simple Tricks)
How to Sum Time in Excel
How to compute sum of x, sum of x squared and mean using a scientific calculator || Stat Tutorials
How to Sum per Month in Excel and add more criteria like Product, Customer etc | Sumifs function
Комментарии
 0:00:38
0:00:38
 0:03:57
0:03:57
 0:10:38
0:10:38
 0:01:02
0:01:02
 0:00:34
0:00:34
 0:02:10
0:02:10
 0:20:24
0:20:24
 0:03:53
0:03:53
 0:07:26
0:07:26
 0:01:11
0:01:11
 0:07:53
0:07:53
 0:00:51
0:00:51
 0:02:54
0:02:54
 0:00:51
0:00:51
 0:01:14
0:01:14
 0:07:39
0:07:39
 0:01:55
0:01:55
 0:02:25
0:02:25
 0:04:53
0:04:53
 0:02:24
0:02:24
 0:00:42
0:00:42
 0:03:07
0:03:07
 0:06:08
0:06:08
 0:05:23
0:05:23