filmov
tv
The Complex Logarithm
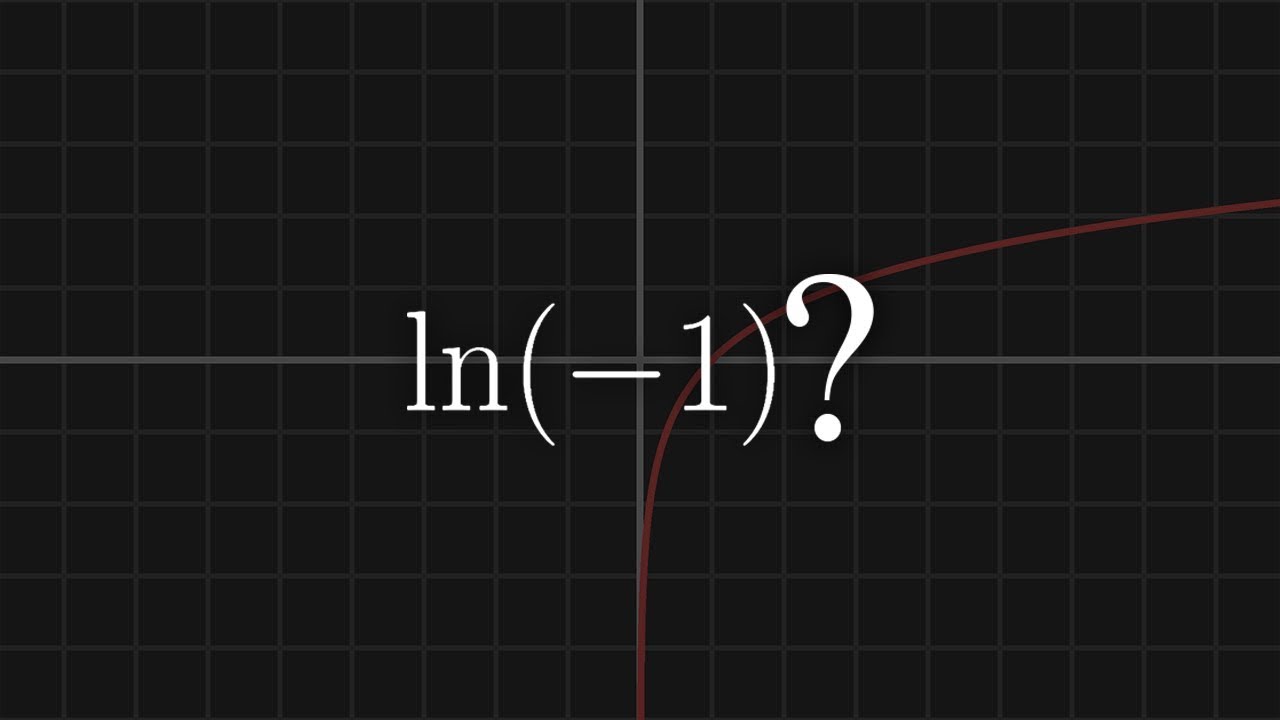
Показать описание
In this video, we cover three central ideas: the natural log of -1, the natural log of any complex number, and the principal log.
I know it's been a while since I've uploaded a video, but I'm now done with high school! Since I'm only starting university in September, I've got a lot of free time to work on more videos. I'm going to try to upload every two (plus or minus 1) weeks.
I know it's been a while since I've uploaded a video, but I'm now done with high school! Since I'm only starting university in September, I've got a lot of free time to work on more videos. I'm going to try to upload every two (plus or minus 1) weeks.
Complex Analysis L04: The Complex Logarithm, Log(z)
The Complex Logarithm
The Complex Logarithm Function | Principal value of the Logarithm | Complex Analysis #5
The fascinating case of the complex logarithm
Complex Analysis 06: The Complex Logarithm
The Complex Logarithm
Computations with the complex logarithm
RSF: multi-valued function example: complex logarithm
EXONENTIAL FORM AND LOGARITHM OF A COMPLX NUMBER
Compute all values of the Complex Logarithm log(i)
How to find All Values of the Complex Logarithm Example
Complex Logarithm
Solving Complex Logarithmic Equations
What is the logarithm of a complex number?
Complex log identites
Simplifying Complex Logarithms
The Complex Logarithm: Multivalued Functions?!?
Complex Logarithm, Branch Points, and Branch Cuts
How to find the logarithm of a complex number
Log 2+2i The Complex Logarithm
Complex logarithm
Principal Branch of the Complex Logarithm
Identities involving the complex logarithm
The Complex Log of -2+2i
Комментарии
 0:28:01
0:28:01
 0:04:06
0:04:06
 0:05:05
0:05:05
 0:17:31
0:17:31
 0:09:14
0:09:14
 0:19:06
0:19:06
 0:05:12
0:05:12
 0:00:20
0:00:20
 0:21:54
0:21:54
 0:02:07
0:02:07
 0:03:05
0:03:05
 0:26:06
0:26:06
 0:10:42
0:10:42
 0:07:14
0:07:14
 0:14:09
0:14:09
 0:09:31
0:09:31
 0:23:18
0:23:18
 0:37:50
0:37:50
 0:05:49
0:05:49
 0:05:22
0:05:22
 0:15:37
0:15:37
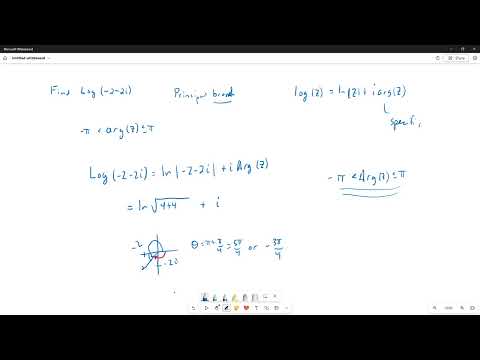 0:05:23
0:05:23
 0:05:27
0:05:27
 0:05:20
0:05:20