filmov
tv
Mastering An Engaging Rational Equation Challenge | Algebra

Показать описание
Mastering An Engaging Rational Equation Challenge | Algebra
Welcome to our latest algebra tutorial where we delve into mastering rational equations! In this engaging video, we'll tackle challenging rational equations step-by-step, providing you with the tools and strategies needed to conquer even the most complex problems. From understanding the fundamentals to mastering advanced techniques, this tutorial is designed to enhance your algebra skills and boost your problem-solving confidence. Whether you're a student looking to ace your next math exam or someone who wants to brush up on algebraic concepts, this video is for you. Get ready to level up your algebra game and become a master of rational equations!
🔮 In this video, you'll discover:
Method to confidently solve rational equation challenge.
Step-by-step guidance on applying magical technique to simplify and solve.
Pro tips for mastering the art of rational equation mastery.
Get ready to command and conquer with this method! 🚀✨ Subscribe now for a journey into the realm of mathematical mastery!
Timestamps:
0:00 Introduction
0:27 Domain
1:20 Algebraic identity
4:28 Substitution
6:27 Quadratic equation
7:52 Quadratic formula
8:20 Solutions
8:45 Verification
#Algebra #Mathematics #RationalEquations #ProblemSolving #MathHelp #MathTutorial #MasteringAlgebra #MathSkills #Education #Learning #StudyTips #MathematicsEducation #MathematicsTutorial #AlgebraTutorial #MathematicsHelp #algebra #maths #mathskills #rational
🔔 Like, share, and subscribe to join our community of mathematical explorers! 🤓🔍✅
We'd love to hear from you! Did you manage to solve the equation? What other math problems would you like us to cover? Let us know in the comments below!
🎓 Happy learning, and see you in the next video! 🎉
Thanks for Watching !!
@infyGyan
Welcome to our latest algebra tutorial where we delve into mastering rational equations! In this engaging video, we'll tackle challenging rational equations step-by-step, providing you with the tools and strategies needed to conquer even the most complex problems. From understanding the fundamentals to mastering advanced techniques, this tutorial is designed to enhance your algebra skills and boost your problem-solving confidence. Whether you're a student looking to ace your next math exam or someone who wants to brush up on algebraic concepts, this video is for you. Get ready to level up your algebra game and become a master of rational equations!
🔮 In this video, you'll discover:
Method to confidently solve rational equation challenge.
Step-by-step guidance on applying magical technique to simplify and solve.
Pro tips for mastering the art of rational equation mastery.
Get ready to command and conquer with this method! 🚀✨ Subscribe now for a journey into the realm of mathematical mastery!
Timestamps:
0:00 Introduction
0:27 Domain
1:20 Algebraic identity
4:28 Substitution
6:27 Quadratic equation
7:52 Quadratic formula
8:20 Solutions
8:45 Verification
#Algebra #Mathematics #RationalEquations #ProblemSolving #MathHelp #MathTutorial #MasteringAlgebra #MathSkills #Education #Learning #StudyTips #MathematicsEducation #MathematicsTutorial #AlgebraTutorial #MathematicsHelp #algebra #maths #mathskills #rational
🔔 Like, share, and subscribe to join our community of mathematical explorers! 🤓🔍✅
We'd love to hear from you! Did you manage to solve the equation? What other math problems would you like us to cover? Let us know in the comments below!
🎓 Happy learning, and see you in the next video! 🎉
Thanks for Watching !!
@infyGyan
Комментарии
 0:11:03
0:11:03
 0:09:53
0:09:53
 0:12:06
0:12:06
 0:08:27
0:08:27
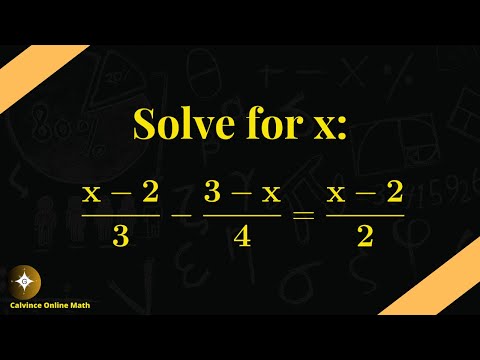 0:01:43
0:01:43
 0:01:00
0:01:00
 0:14:58
0:14:58
 0:01:00
0:01:00
 0:13:17
0:13:17
 0:11:07
0:11:07
 0:07:11
0:07:11
 0:05:17
0:05:17
 0:00:57
0:00:57
 0:00:48
0:00:48
 0:05:58
0:05:58
 0:00:18
0:00:18
 0:00:32
0:00:32
 0:15:42
0:15:42
 0:05:36
0:05:36
 0:08:56
0:08:56
 0:18:45
0:18:45
 0:00:13
0:00:13
 0:00:44
0:00:44
 0:00:33
0:00:33