filmov
tv
Understanding the Process of Multiplication and Division of Rational Expressions

Показать описание
Multiplication and division of rational expressions involve applying principles from algebra to combine or simplify fractions with variables. When multiplying, multiply the numerators and denominators separately, then simplify by factoring and canceling common factors. For division, multiply by the reciprocal of the divisor, turning the problem into multiplication. Simplify further by factoring and canceling common factors. Rational expressions involve algebraic fractions, and mastering these operations is crucial for simplifying complex expressions and solving equations involving rational functions. These skills are foundational for advanced algebra and calculus, providing a basis for more intricate mathematical concepts.
Math Antics - Multi-Digit Multiplication Pt 1
2-Digit by 2-Digit Multiplication | Math with Mr. J
Math - Long Multiplication
Understanding the Process of Multiplication and Division of Rational Expressions
Fast Multiplication Tricks 2 Digit Numbers
The Fastest Way to Learn Multiplication Facts
Multiplication for Kids
How To Multiply with Decimals #decimals #multiplication #decimalmultiplication #math #silentmath
Fast Multiplication Trick | Interesting math tricks #maths #shorts
Math Antics - Multi-Digit Multiplication Pt 2
What is Multiplication? | Multiplication Concepts for Kids | Rock 'N Learn
JAPANESE MULTIPLICATION/ How to multiply by JAPANESE method
quick multiplication process 😁 #viralvideo #shortsvideo #maths #mathstricks #mathematics
2 Digit Multiplication easily | Brain Games | Brain Development
Japanese Multiplication - Using Lines
Multiplication 3rd Grade - Learn Multiplication Educational Math Videos
maths always easy. quick multiplication process
Lattice Multiplication 😳 #Shorts #math #maths #mathematics #multiplication #education #learn
Multiplying 2 digit numbers- example 1
Multiplication Lattice Method
Fast Multiplication Trick | Interesting math tricks #shorts #magic #trending
Multiplication trick #shorts #maths
2-Digit by 2-Digit Multiplication Math - How to Multiply a 2-Digit Number
Multiplication Tricks To Make Mathematics Fun and Easy 😉 #math #multiplication #mathtrick
Комментарии
 0:06:05
0:06:05
 0:04:54
0:04:54
 0:06:26
0:06:26
 0:01:00
0:01:00
 0:00:34
0:00:34
 0:06:04
0:06:04
 0:09:53
0:09:53
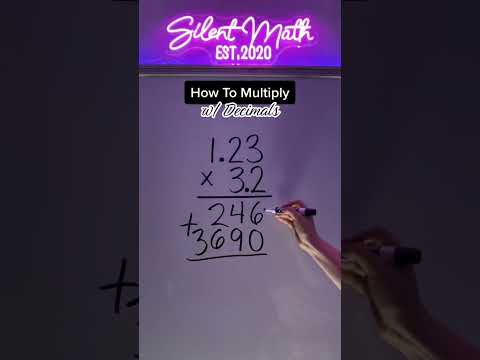 0:00:37
0:00:37
 0:00:28
0:00:28
 0:08:24
0:08:24
 0:10:54
0:10:54
 0:00:28
0:00:28
 0:00:26
0:00:26
 0:05:49
0:05:49
 0:01:30
0:01:30
 0:03:44
0:03:44
 0:00:27
0:00:27
 0:00:36
0:00:36
 0:03:12
0:03:12
 0:00:58
0:00:58
 0:00:17
0:00:17
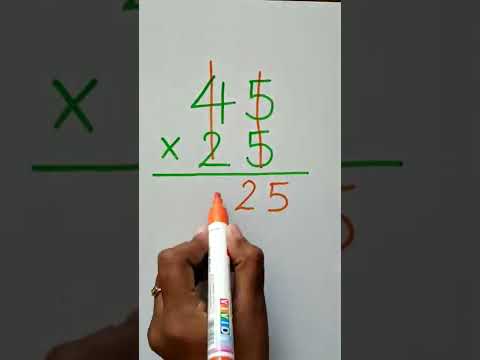 0:00:12
0:00:12
 0:04:11
0:04:11
 0:00:17
0:00:17