filmov
tv
Algebraic Approach to this one
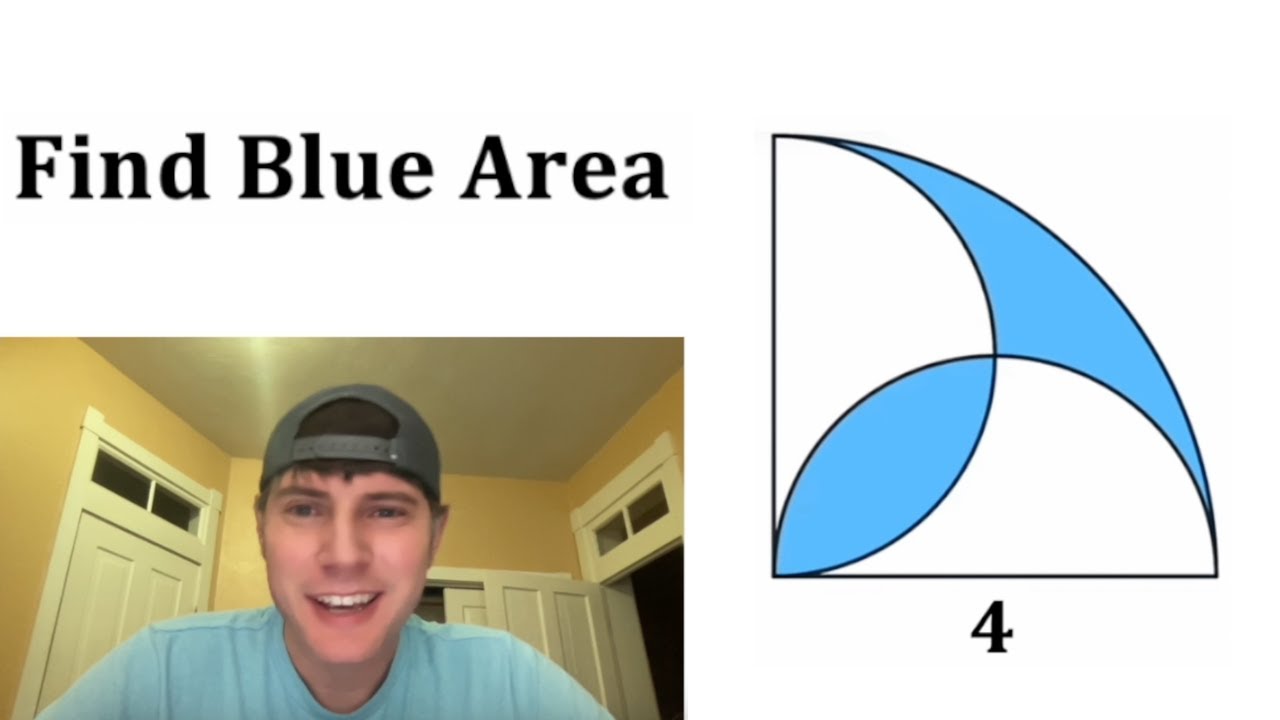
Показать описание
I wanted to try this one with this algebraic approach. It was fun to go through.
Algebraic Approach to this one
Finding Limits an Algebraic Approach
01 - Introduction to the Algebraic Method for Balancing Chemical Equations
Algebra: FOIL Method #Shorts #algebra #math #maths #mathematics #education #learn
Lesson 1.3 - Analysis of Functions - Algebraic Approach
functions explained in 17 seconds! (Algebra 1)
Basic Algebra Tips
An Introduction to an Algebraic Approach to Limits ♦︎ Calculus 1
Per Calculus | LIMIT OF A FUNCTION | Substitution Method | #limit #calculus #ganiyuabubakar
Algebra Basics: Solving 2-Step Equations - Math Antics
How to Determine if a Function is One-to-One Algebraically
Solving Systems of Equations By Elimination & Substitution With 2 Variables
How to show that a Function is One-to-One algebraically | SHS 1 ELECTIVE MATH
02 - Algebraic Method for Balancing Chemical Equations (Example #1)
Multiplication of algebraic expression | Algebraic expression class 8 | Algebraic expression|#shorts
x+1/x Tricks for competitive exams | Algebra Questions for SSC CGL NTPC Railway Exams
Mathematics 1 Algebraic Approach 1
Algebra - How To Solve Equations Quickly!
Infinite Limit Shortcut!! (Calculus)
Algebra for Beginners | Basics of Algebra
🤔How to simplify algebraic expressions??? Algebraic Expressions/Short Tricks #shorts #shortsfeed
Logarithmic Form to Exponential Form (Natural Log Edition) 🤯 #Shorts #algebra #math #education
Simplifying Expressions / Collecting like terms / Algebra
Factoring by Grouping Example 😎 #Shorts #algebra #math #maths #mathematics
Комментарии
 0:03:38
0:03:38
 0:07:41
0:07:41
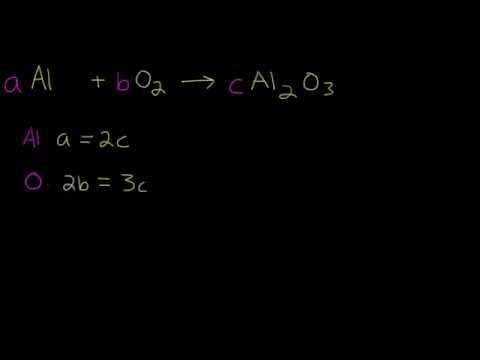 0:03:56
0:03:56
 0:00:18
0:00:18
 0:14:06
0:14:06
 0:00:21
0:00:21
 0:00:48
0:00:48
 0:12:35
0:12:35
 0:23:39
0:23:39
 0:10:29
0:10:29
 0:13:56
0:13:56
 0:10:27
0:10:27
 0:10:33
0:10:33
 0:03:25
0:03:25
 0:00:19
0:00:19
 0:00:24
0:00:24
 0:10:12
0:10:12
 0:25:05
0:25:05
 0:00:51
0:00:51
 0:37:09
0:37:09
 0:00:16
0:00:16
 0:00:28
0:00:28
 0:00:06
0:00:06
 0:00:27
0:00:27