The Norm of a Vector

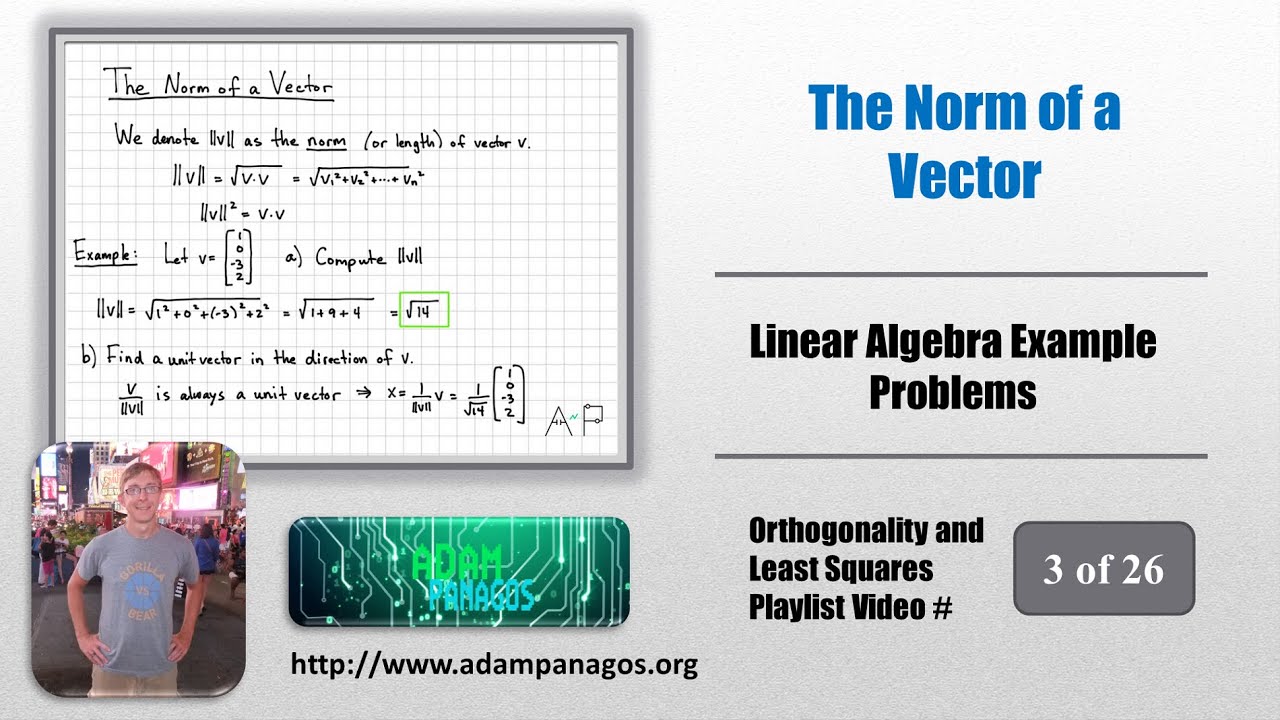
The norm of a vector provides a measure of vector size. For the case of vectors in Rn, this vector norm is the length of the vector and the vector norm is defined as the square-root of the dot product of the vector with itself. We show how this norm definition works for the case of vectors in Rn, and also provide an example of computing the norm of a vector. An example of finding a unit vector in a desired direction is also provided. This establishes a useful fact that a vector divided by its norm is always a unit vector.

The next video in this playlist is:

The previous video in this playlist is:

The full playlist of 26 videos on Orthogonality and Least Squares is here:

Course website:

Join the YouTube channel for membership perks:

[cherinhalechantry]

I have just subscribed to your channel. You have explained it in plain and simple terms. Thank you!

[namgaydorji]

Thank you very much, sir. I found your instruction on the norm of a vector to be highly efficient, and I have subscribed to your channel. I hope you keep these gems coming.