filmov
tv
Lecture 8: Norms of Vectors and Matrices

Показать описание
MIT 18.065 Matrix Methods in Data Analysis, Signal Processing, and Machine Learning, Spring 2018
Instructor: Gilbert Strang
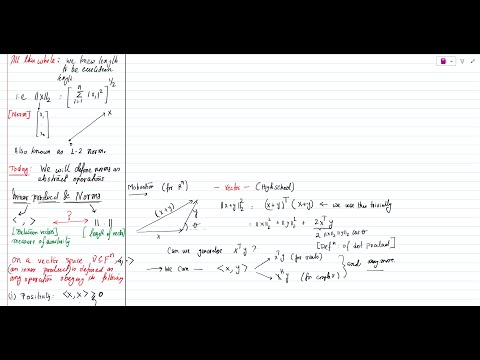
A norm is a way to measure the size of a vector, a matrix, a tensor, or a function. Professor Strang reviews a variety of norms that are important to understand including S-norms, the nuclear norm, and the Frobenius norm.
License: Creative Commons BY-NC-SA
Instructor: Gilbert Strang
A norm is a way to measure the size of a vector, a matrix, a tensor, or a function. Professor Strang reviews a variety of norms that are important to understand including S-norms, the nuclear norm, and the Frobenius norm.
License: Creative Commons BY-NC-SA
Lecture 8: Norms of Vectors and Matrices
EECS - Module 8 - Induced Norms
Numerical Methods: Vector and Matrix Norms
Linear Algebra: Norm
2.1 Vector norms and matrix norms
Session 8: Inner products, vector norms, dual spaces, introduction to matrix norms
Advanced Linear Algebra, Lecture 5.7: The norm of a linear map
1 3 8 Submultiplicative norms
Vector Norms - Linear Algebra
The Lp Norm for Vectors and Functions
Norms of Vectors and Matrices
MaDL - Vector and Matrix Norms
01.3.8 Submultiplicative norms
MATH426: Vector norms
Lecture 8: Inner Product Spaces and Norms
Part 8 - Norm of a Vector
Linear Algebra, Lesson 5, Video 8: Proof of Homogeniety of Two Norm
Matrix Norms : Data Science Basics
1-2 Vector and matrix norms
3.3.7-Linear Algebra: Vector and Matrix Norms
1.3.4 Induced matrix norms
What is Norm in Machine Learning?
norm of a vector in R2
01.2.3 The 2 norm
Комментарии
 0:49:21
0:49:21
 0:22:20
0:22:20
 0:10:57
0:10:57
 0:31:21
0:31:21
 0:06:52
0:06:52
 2:43:07
2:43:07
 0:47:07
0:47:07
 0:03:18
0:03:18
 0:06:06
0:06:06
 0:09:34
0:09:34
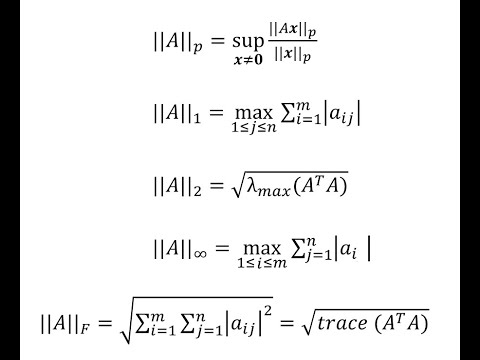 0:17:16
0:17:16
 0:05:14
0:05:14
 0:03:30
0:03:30
 0:09:33
0:09:33
 0:47:53
0:47:53
 0:07:50
0:07:50
 0:12:00
0:12:00
 0:09:57
0:09:57
 0:25:45
0:25:45
 0:04:01
0:04:01
 0:09:16
0:09:16
 0:05:15
0:05:15
 0:02:57
0:02:57
 0:05:42
0:05:42