Proof: Sequence Order Limit Theorem (Inequalities and Limits) | Real Analysis

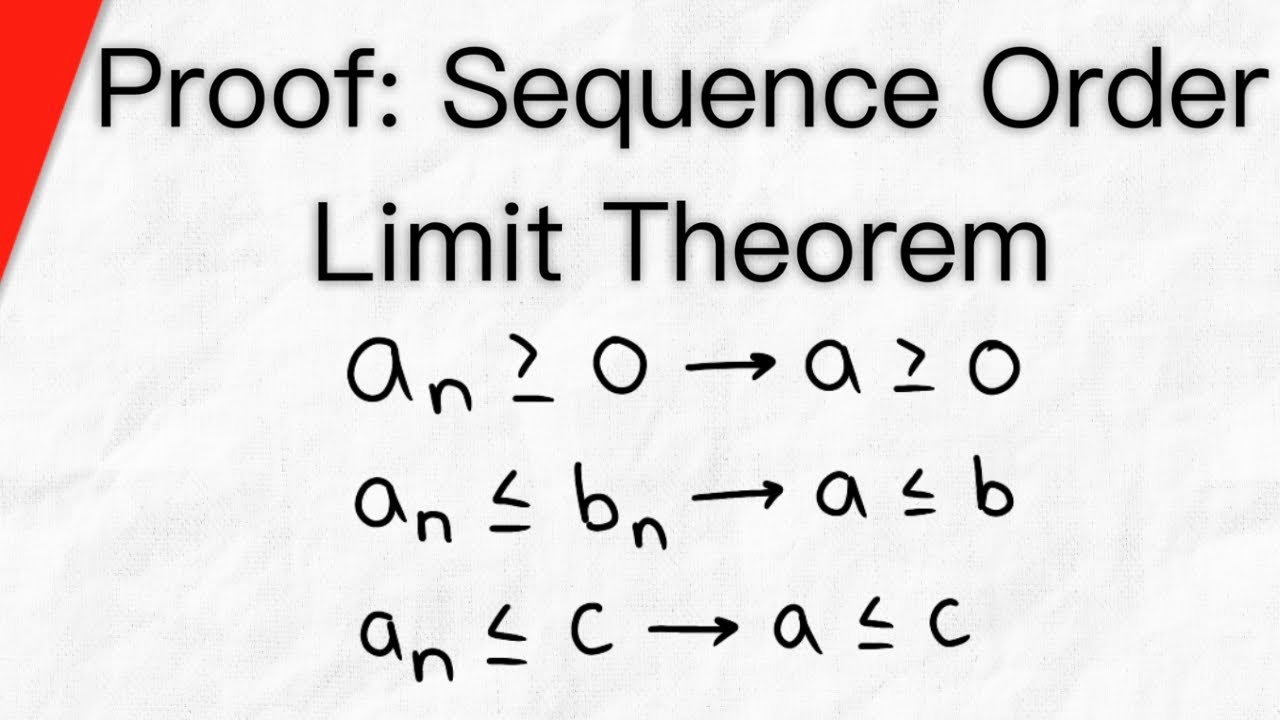
preview_player
Показать описание
We prove the order limit theorem for convergent sequences. This proves that convergent sequences and their limits relate to each other and real numbers as we'd expect. For example if a_n converges to a and b_n converges to b, and every a_n is less than or equal to each b_n, then a is less than or equal to b. This theorem summarizes how inequalities behave with limits. #realanalysis

★DONATE★

Thanks to Robert Rennie and Barbara Sharrock for their generous support on Patreon!

Follow Wrath of Math on...

  1. Wrath of Math
  2. wrath of math
  3. math lessons
  4. math
  5. education
  6. math video
Рекомендации по теме
Proof: Sequence Order 0:11:36

Proof: Sequence Order Limit Theorem (Inequalities and Limits) | Real Analysis

Order limit theorem 0:09:25

Order limit theorem

6.2 Order Limit 0:07:22

6.2 Order Limit Theorem

Order Limit Theorem 0:05:44

Order Limit Theorem - Real Analysis

Proof: Sequence (3n+1)/(n+2) 0:06:53

Proof: Sequence (3n+1)/(n+2) Converges to 3 | Real Analysis

Math 441 - 0:22:54

Math 441 - 2.3 Algebraic and Order Limit Theorems

Proof: Central Limit 0:35:14

Proof: Central Limit Proof

The Limit of 0:05:14

The Limit of a Sequence is Unique Proof

Proof: The Limit 0:13:22

Proof: The Limit of a Sequence is Unique | Real Analysis

Definition of the 0:13:59

Definition of the Limit of a Sequence | Real Analysis

Why greatest Mathematicians 0:00:38

Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths

6-1 Algebraic Limit 0:47:37

6-1 Algebraic Limit Theorem

Real Analysis Course 0:05:35

Real Analysis Course #18 - Sequence Limits are Unique Proof

Real Analysis 4 0:06:53

Real Analysis 4 | Theorem on Limits

Algebraic Limit Theorem 0:02:36

Algebraic Limit Theorem (part 1 of 4)(multiplication with constant) Proof

2.3 The Algebraic 0:16:04

2.3 The Algebraic and Order Limit Theorems: OLT

Proof: Limit Arithmetics 0:26:00

Proof: Limit Arithmetics Theorem, With Visualization

The Central Limit 0:06:05

The Central Limit Theorem

Proof: Limit Law 0:07:56

Proof: Limit Law for Sum of Convergent Sequences | Real Analysis

Proof: Limit Law 0:05:21

Proof: Limit Law for Constant Times a Convergent Sequence | Real Analysis

Algebraic Limit Theorem 0:02:42

Algebraic Limit Theorem (part 2 of 4)(addition) Proof

Proof: Limit Law 0:16:31

Proof: Limit Law for Quotient of Convergent Sequences | Real Analysis

Connecting Function Limits 0:12:22

Connecting Function Limits and Sequence Limits | Real Analysis

Lecture 4.1 - 0:11:45

Lecture 4.1 - Limit Theorems for Sequences

Комментарии
Автор

how should i come to the assumption and let e = |a|

KhloudAhmed-fclj
Автор

Hi why did you replace the a(n) by a(N) at 4:36, wouldn't it have still been correct if we continued with a(n)?

michaelhunt
Автор

Hey sir I have a question for a code question reckon you could help - For the first two digits use an odd number between 39 and 100, for the last two digits use a multiple of 10, repetition is allowed work out the total number of codes which can be made using the method

louiesaunders