Area Enclosed by Curve and y Axis Formula and Explanation - Integrals and Integration - IB AA HL

To calculate the area enclosed by a curve and the y axis using integration we start by writing the curve's equation y=f(x) as a function of y, thereby making x the subject x=g(y).
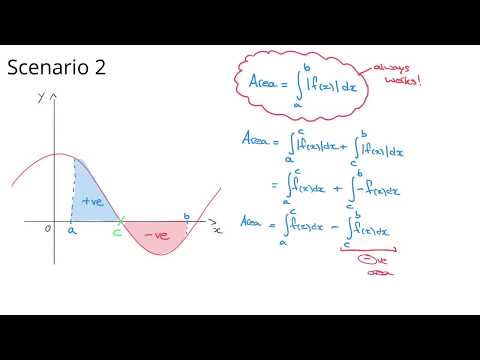
Then we distinguish 2 scenarios:
scenario 1 : all of the x coordinates along the curve are greater than or equal to zero 0. In this case the area equals to the definite integral from c to d of the function x = g(y)
scenario 2 : some of the x coordinates along the curve are negative. In this case the area equals to the definite integral from c to d of the absolute value of the function x = g(y).