filmov
tv
Tricky Algebra Problem Using FOIL Polynomials & Quadratics SAT & ACT Math Prep #shorts #maths #math
Показать описание
Tricky Algebra Problem Using FOIL Polynomials & Quadratics SAT & ACT Math Prep #shorts #mat...
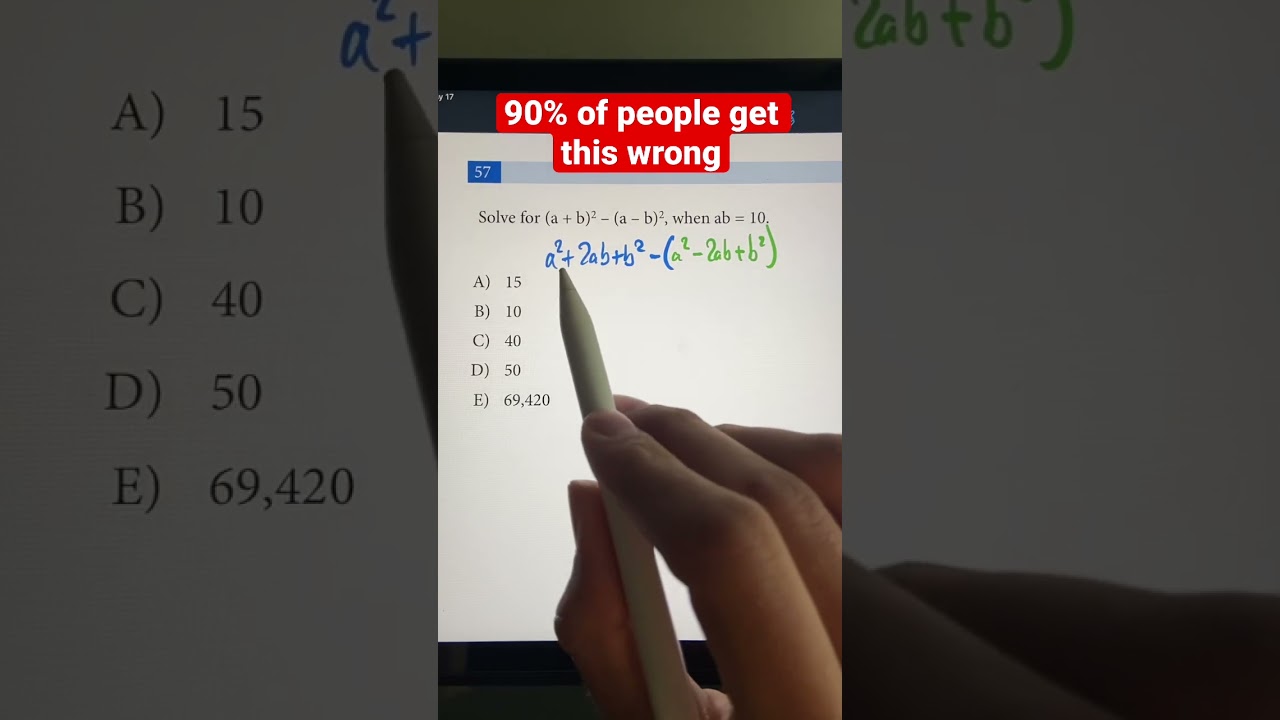
Tricky Algebra Problem Using FOIL Polynomials & Quadratics.
How to Factor Trinomials with Reverse FOIL (Simple AC Algorithm Method when a is not 1)
Tricky Algebra Problem using Foil Polynomial #quadraticidentities #mathsshort#algebramaths
Factor Trinomials with Reverse FOIL (Simple AC Algorithm Method when a is not 1)
Tricky Algebra Problem Using FOIL Polynomials & Quadratics Algebra Maths Prep #shorts #maths #le...
Polynomials & Quadratics Math | Tricky Algebra Problem Using FOIL #shorts #maths #math
The FOIL Method | Easiest way to Multiply Polynomials | Algebra
Factor Trinomials with Reverse FOIL (Simple AC Algorithm Method when a is not 1)
Tricky Algebra Problem Using FOIL Polynomials & Quadratics SAT & ACT Math Prep in Telugu #sh...
GED Math FOIL and Factor!
How to Use FOIL to Multiply Binomials - Polynomial
ADD the F.O.I.L. METHOD to your Basic Algebra Toolbox
FOIL Example - Hard
'Efficiently Master the FOIL Method for Binomial Multiplication' #SHORTS #math #problems #...
Foil Method Algebra, Binomials, Trinomials, Polynomials, Multiplication With Exponents
Trickiest Algebra Problem - Can you Solve it?? Using Foil Polynomials - #math #shorts #GSshorts
Expanding Brackets
Let’s Multiply Polynomials Using FOIL …. Step-by-Step…..
Solve this quadratic equation using the FOIL method!😊 #shorts #gmat
How to Solve FOIL Questions (easy to hard)
FASTEST way to factor a trinomial! #shorts
Multiplying Binomials by the FOIL Method
YOU DECIDE: u-substitution or foil method?? #calculus #calculushelp #mathematics #integrals
Комментарии
 0:00:52
0:00:52
 0:00:48
0:00:48
 0:03:20
0:03:20
 0:00:53
0:00:53
 0:05:12
0:05:12
 0:00:51
0:00:51
 0:01:00
0:01:00
 0:03:26
0:03:26
 0:06:13
0:06:13
 0:00:58
0:00:58
 0:06:10
0:06:10
 0:03:36
0:03:36
 0:14:32
0:14:32
 0:01:44
0:01:44
 0:00:59
0:00:59
 0:18:09
0:18:09
 0:00:57
0:00:57
 0:00:51
0:00:51
 0:12:40
0:12:40
 0:01:00
0:01:00
 0:35:16
0:35:16
 0:00:55
0:00:55
 0:06:25
0:06:25
 0:00:35
0:00:35