filmov
tv
Partial Derivatives - Trigonometric Functions

Показать описание
Partial Derivatives - Trigonometric Functions
Here is an introductory example of how a partial derivative is calculated. In this example we use a trigonometric function.
Now that we have the brief discussion on limits out of the way we can proceed into taking derivatives of functions of more than one variable. Before we actually start taking derivatives of functions of more than one variable let’s recall an important interpretation of derivatives of functions of one variable.
Recall that given a function of one variable, , the derivative, , represents the rate of change of the function as x changes. This is an important interpretation of derivatives and we are not going to want to lose it with functions of more than one variable. The problem with functions of more than one variable is that there is more than one variable. In other words, what do we do if we only want one of the variables to change, or if we want more than one of them to change? In fact, if we’re going to allow more than one of the variables to change there are then going to be an infinite amount of ways for them to change. For instance, one variable could be changing faster than the other variable(s) in the function. Notice as well that it will be completely possible for the function to be changing differently depending on how we allow one or more of the variables to change.
We will need to develop ways, and notations, for dealing with all of these cases. In this section we are going to concentrate exclusively on only changing one of the variables at a time, while the remaining variable(s) are held fixed. We will deal with allowing multiple variables to change in a later section.
Because we are going to only allow one of the variables to change taking the derivative will now become a fairly simple process.
Note that these two partial derivatives are sometimes called the first order partial derivatives. Just as with functions of one variable we can have derivatives of all orders. We will be looking at higher order derivatives in a later section.
Note that the notation for partial derivatives is different than that for derivatives of functions of a single variable. With functions of a single variable we could denote the derivative with a single prime. However, with partial derivatives we will always need to remember the variable that we are differentiating with respect to and so we will subscript the variable that we differentiated with respect to. We will shortly be seeing some alternate notation for partial derivatives as well.
Here is an introductory example of how a partial derivative is calculated. In this example we use a trigonometric function.
Now that we have the brief discussion on limits out of the way we can proceed into taking derivatives of functions of more than one variable. Before we actually start taking derivatives of functions of more than one variable let’s recall an important interpretation of derivatives of functions of one variable.
Recall that given a function of one variable, , the derivative, , represents the rate of change of the function as x changes. This is an important interpretation of derivatives and we are not going to want to lose it with functions of more than one variable. The problem with functions of more than one variable is that there is more than one variable. In other words, what do we do if we only want one of the variables to change, or if we want more than one of them to change? In fact, if we’re going to allow more than one of the variables to change there are then going to be an infinite amount of ways for them to change. For instance, one variable could be changing faster than the other variable(s) in the function. Notice as well that it will be completely possible for the function to be changing differently depending on how we allow one or more of the variables to change.
We will need to develop ways, and notations, for dealing with all of these cases. In this section we are going to concentrate exclusively on only changing one of the variables at a time, while the remaining variable(s) are held fixed. We will deal with allowing multiple variables to change in a later section.
Because we are going to only allow one of the variables to change taking the derivative will now become a fairly simple process.
Note that these two partial derivatives are sometimes called the first order partial derivatives. Just as with functions of one variable we can have derivatives of all orders. We will be looking at higher order derivatives in a later section.
Note that the notation for partial derivatives is different than that for derivatives of functions of a single variable. With functions of a single variable we could denote the derivative with a single prime. However, with partial derivatives we will always need to remember the variable that we are differentiating with respect to and so we will subscript the variable that we differentiated with respect to. We will shortly be seeing some alternate notation for partial derivatives as well.
Комментарии
 0:07:50
0:07:50
 0:07:11
0:07:11
 0:01:32
0:01:32
 0:05:58
0:05:58
 1:00:33
1:00:33
 0:01:30
0:01:30
 0:05:22
0:05:22
 0:06:11
0:06:11
 0:03:56
0:03:56
 0:03:48
0:03:48
 0:02:38
0:02:38
 0:04:48
0:04:48
 0:05:17
0:05:17
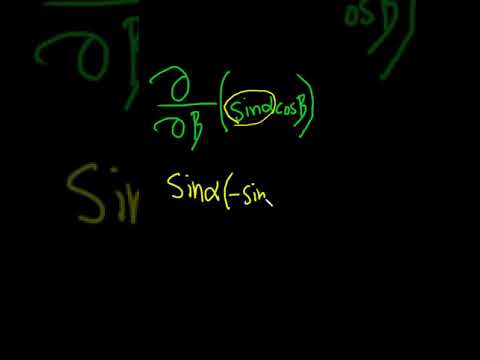 0:00:42
0:00:42
 0:17:04
0:17:04
 0:00:42
0:00:42
 0:01:39
0:01:39
 0:00:43
0:00:43
 0:04:33
0:04:33
 0:07:42
0:07:42
 0:10:08
0:10:08
 0:06:19
0:06:19
 0:00:22
0:00:22
 0:00:44
0:00:44