filmov
tv
Complex Analysis - 34: Laurent Series - 3

Показать описание
We derive Cauchy Integral Formula for an annulus and prove the existence and uniqueness of the Laurent decomposition. We then arrive at the Laurent series, prove its uniqueness and the Cauchy estimates.
Timestamp provided by Priyanka Vaidheesh.
0:00 Aim of the lecture.
02:17 Recap of CIF for holomorphic function in a open disc .
05:30 Cauchy Integral formula for holomorphic function in an annulus.
14:35 Laurent decomposition of holomorphic function in an annular region.
27:00 Laurent series expansion of Laurent decomposition.
42:17 Coefficients of Lurents series and the nature of singularity.
49:40 End note of lecture.
Timestamp provided by Priyanka Vaidheesh.
0:00 Aim of the lecture.
02:17 Recap of CIF for holomorphic function in a open disc .
05:30 Cauchy Integral formula for holomorphic function in an annulus.
14:35 Laurent decomposition of holomorphic function in an annular region.
27:00 Laurent series expansion of Laurent decomposition.
42:17 Coefficients of Lurents series and the nature of singularity.
49:40 End note of lecture.
 0:51:12
0:51:12
 0:19:49
0:19:49
 0:21:39
0:21:39
 0:21:38
0:21:38
 0:37:20
0:37:20
 0:08:26
0:08:26
 0:28:20
0:28:20
 0:18:49
0:18:49
 0:22:29
0:22:29
 0:18:10
0:18:10
 0:55:15
0:55:15
 0:24:51
0:24:51
 0:16:43
0:16:43
 0:56:28
0:56:28
 0:05:20
0:05:20
 0:55:47
0:55:47
 0:06:40
0:06:40
 0:06:44
0:06:44
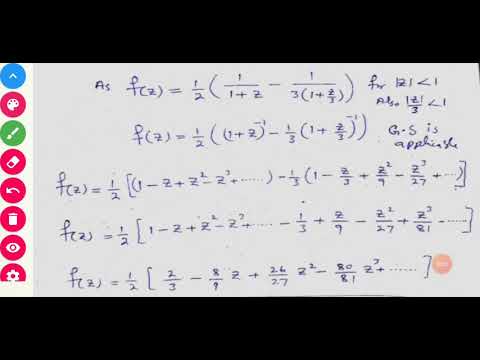 0:22:02
0:22:02
 0:55:30
0:55:30
 0:28:38
0:28:38
 0:12:40
0:12:40
 0:04:05
0:04:05
 0:10:34
0:10:34