filmov
tv
Discrete gradient vector fields on simplicial complexes and rooted forests (Ivan Contreras Palacios)

Показать описание
Discrete Math Seminar on October 15, 2021
Abstract: Discrete Morse theory was originally formulated by R. Forman in 1998 as a CW-complex version of smooth Morse theory. In this talk we use a generalization of the graph Laplacian in simplicial complexes to find a generating function for the number of discrete gradient vector fields, in the case when the complex is a triangulation of an orientable manifold. We characterize a correspondence between discrete gradient vector fields for Morse functions and higher dimensional rooted forests of simplicial complexes. Based on joint work with Andrew Tawfeek (arXiv:2105.05388)
Abstract: Discrete Morse theory was originally formulated by R. Forman in 1998 as a CW-complex version of smooth Morse theory. In this talk we use a generalization of the graph Laplacian in simplicial complexes to find a generating function for the number of discrete gradient vector fields, in the case when the complex is a triangulation of an orientable manifold. We characterize a correspondence between discrete gradient vector fields for Morse functions and higher dimensional rooted forests of simplicial complexes. Based on joint work with Andrew Tawfeek (arXiv:2105.05388)
 1:05:42
1:05:42
 0:30:54
0:30:54
 0:04:53
0:04:53
 0:02:18
0:02:18
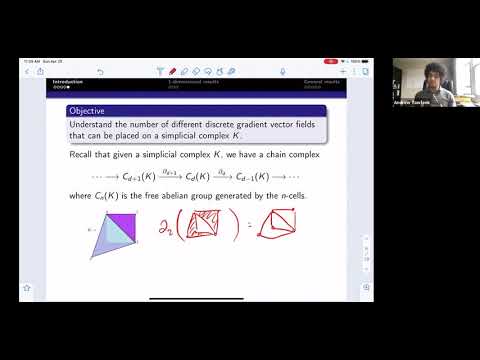 0:21:56
0:21:56
 0:14:51
0:14:51
 0:54:46
0:54:46
 0:06:17
0:06:17
 1:12:47
1:12:47
 0:15:36
0:15:36
 0:21:00
0:21:00
 0:05:30
0:05:30
 0:12:06
0:12:06
 0:09:26
0:09:26
 0:05:31
0:05:31
 0:15:42
0:15:42
 0:12:09
0:12:09
 0:11:24
0:11:24
 0:10:28
0:10:28
 0:08:40
0:08:40
 1:05:45
1:05:45
 1:10:20
1:10:20
 0:03:00
0:03:00
 0:08:26
0:08:26