filmov
tv
Centroid of Composite Bodies: Statics Example.
Показать описание
Description:
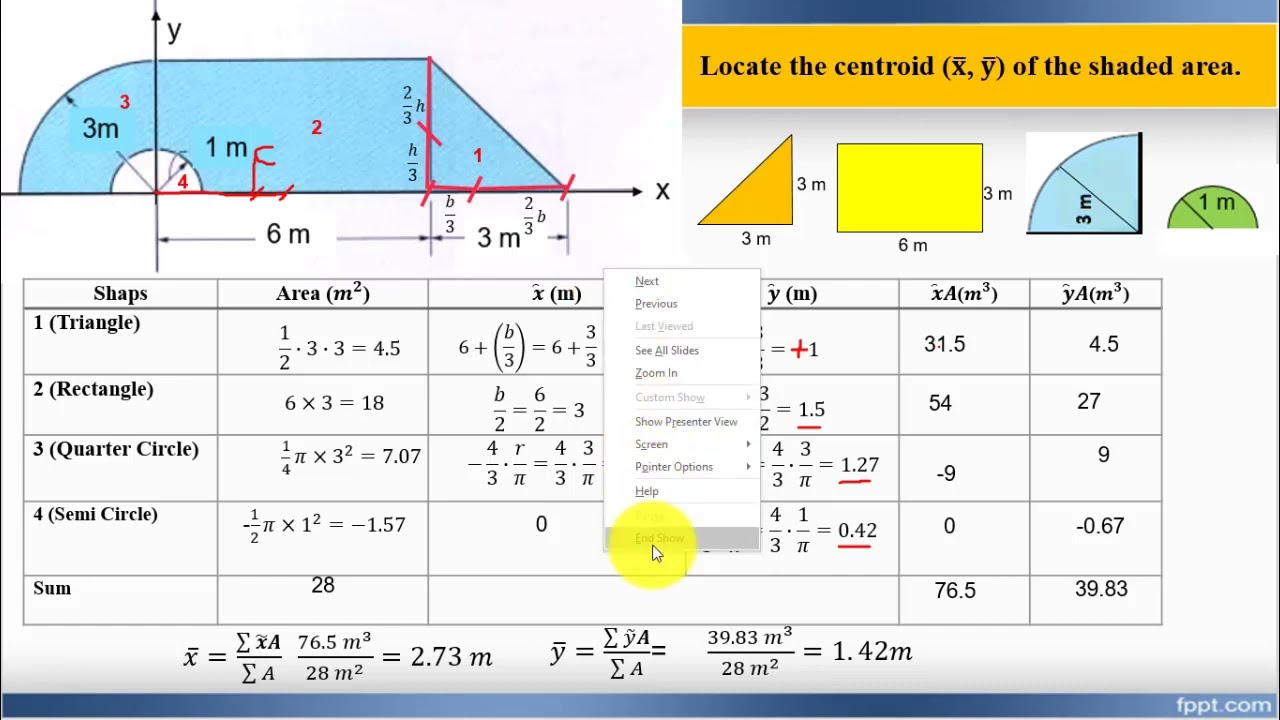
In this engineering mechanics tutorial, we walk through calculating the centroid (X̄ and Ȳ coordinates) of a composite shape consisting of triangles, rectangles, and circular segments. Understanding how to locate the centroid of complex shapes is a fundamental skill for students and professionals in various engineering fields.
We break down the problem-solving approach into the following key steps:
1) Dividing the composite shape into simpler, known shapes (triangle, rectangle, quarter circle, and semicircle)
2) Preparing a table to organize the data for each shape, including area, X̄, Ȳ, X̄ × Area, and Ȳ × Area
3) Calculating the area of each individual shape using appropriate formulas
- Assigning negative areas for unshaded or subtracted sections (e.g., the semicircle)
4) Determining the X̄ and Ȳ coordinates of each shape's centroid relative to the chosen origin
- Using geometric properties and centroid formulas for each shape type
5) Calculating the X̄ × Area and Ȳ × Area values for each shape
6) Summing up the areas, X̄ × Area, and Ȳ × Area values for all shapes
7) Using the centroid formulas to calculate the centroid of the composite shape:
X̄ = Σ(X̄ × Area) ÷ ΣArea
Ȳ = Σ(Ȳ × Area) ÷ ΣArea
By following along with this detailed tutorial, you'll gain a solid understanding of how to approach centroid calculations for composite shapes, breaking down the problem into manageable steps. Perfect for students in engineering mechanics courses and professionals who need to refresh their knowledge of this essential concept.
#EngineeringMechanics #Centroid #CompositeShapes #ProblemSolving #StructuralAnalysis #CivilEngineering #MechanicalEngineering
In this engineering mechanics tutorial, we walk through calculating the centroid (X̄ and Ȳ coordinates) of a composite shape consisting of triangles, rectangles, and circular segments. Understanding how to locate the centroid of complex shapes is a fundamental skill for students and professionals in various engineering fields.
We break down the problem-solving approach into the following key steps:
1) Dividing the composite shape into simpler, known shapes (triangle, rectangle, quarter circle, and semicircle)
2) Preparing a table to organize the data for each shape, including area, X̄, Ȳ, X̄ × Area, and Ȳ × Area
3) Calculating the area of each individual shape using appropriate formulas
- Assigning negative areas for unshaded or subtracted sections (e.g., the semicircle)
4) Determining the X̄ and Ȳ coordinates of each shape's centroid relative to the chosen origin
- Using geometric properties and centroid formulas for each shape type
5) Calculating the X̄ × Area and Ȳ × Area values for each shape
6) Summing up the areas, X̄ × Area, and Ȳ × Area values for all shapes
7) Using the centroid formulas to calculate the centroid of the composite shape:
X̄ = Σ(X̄ × Area) ÷ ΣArea
Ȳ = Σ(Ȳ × Area) ÷ ΣArea
By following along with this detailed tutorial, you'll gain a solid understanding of how to approach centroid calculations for composite shapes, breaking down the problem into manageable steps. Perfect for students in engineering mechanics courses and professionals who need to refresh their knowledge of this essential concept.
#EngineeringMechanics #Centroid #CompositeShapes #ProblemSolving #StructuralAnalysis #CivilEngineering #MechanicalEngineering
 0:08:45
0:08:45
 0:09:26
0:09:26
 0:02:07
0:02:07
 0:08:25
0:08:25
 0:10:35
0:10:35
 0:10:00
0:10:00
 0:06:20
0:06:20
 0:14:00
0:14:00
 0:13:59
0:13:59
 0:15:09
0:15:09
 0:15:19
0:15:19
 0:07:57
0:07:57
 0:15:28
0:15:28
 0:08:55
0:08:55
 0:23:54
0:23:54
 0:06:48
0:06:48
 0:15:45
0:15:45
 0:07:35
0:07:35
 0:13:00
0:13:00
 0:05:19
0:05:19
 0:12:39
0:12:39
 0:21:52
0:21:52
 0:12:43
0:12:43
 0:13:46
0:13:46