filmov
tv
Introduction to the Fourier Transform (Edited)
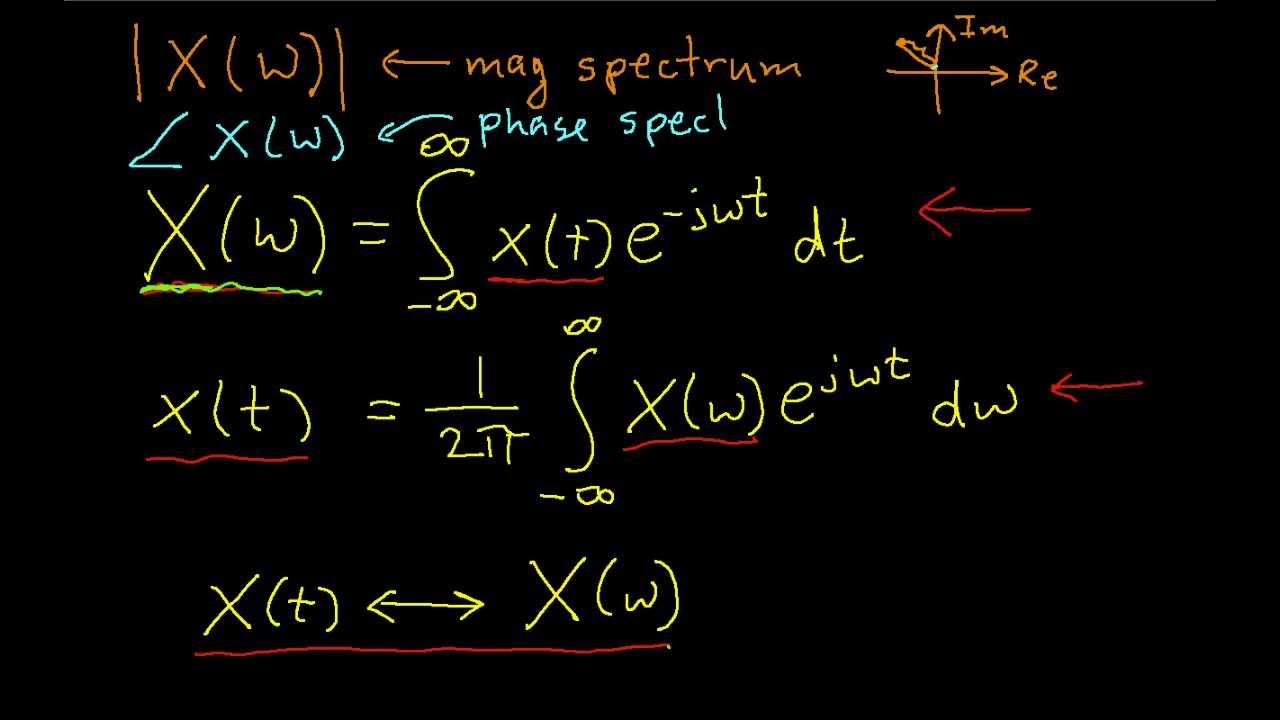
Показать описание
This video is made available under the Creative Commons BY-SA license.
But what is the Fourier Transform? A visual introduction.
Introduction to the Fourier Transform (Part 1)
An Introduction to the Fourier Transform
Introduction to Fourier Transform
Introduction to Fourier Transform
Fourier Transform Equation Explained ('Best explanation of the Fourier Transform on all of YouT...
Fourier Series introduction
Intro to FOURIER SERIES: The Big Idea
Introduction to Signal & Systems L1 | GATE/PSU EC, EE & IN lectures | Online Coaching | Live...
Introduction to the Fourier Transform
Introduction to the Fourier Transform (Part 2)
Introduction to Fourier Series
The Fourier Series and Fourier Transform Demystified
Electrical Engineering: Ch 19: Fourier Transform (1 of 45) What is a Fourier Transform?
William Cox: An Intuitive Introduction to the Fourier Transform and FFT
Fourier Transform, Fourier Series, and frequency spectrum
INTRODUCTION TO FOURIER SERIES PART 1
Time Series, Signals, & the Fourier Transform | Introduction
Fourier Analysis: Overview
Introduction to the Fourier Transform (Edited)
Why do we use the Fourier Transform?
Intro to Fourier transforms: how to calculate them
The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever?
Discrete Fourier Transform - Simple Step by Step
Комментарии
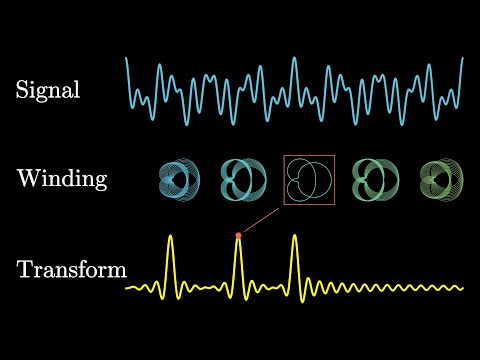 0:20:57
0:20:57
 0:13:03
0:13:03
 0:03:20
0:03:20
 0:06:22
0:06:22
 0:08:19
0:08:19
 0:06:26
0:06:26
 0:05:12
0:05:12
 0:10:44
0:10:44
 1:08:58
1:08:58
 0:10:38
0:10:38
 0:12:57
0:12:57
 0:22:52
0:22:52
 0:14:48
0:14:48
 0:06:21
0:06:21
 0:32:57
0:32:57
 0:15:46
0:15:46
 0:16:03
0:16:03
 0:08:03
0:08:03
 0:07:29
0:07:29
 0:09:02
0:09:02
 0:00:59
0:00:59
 0:22:07
0:22:07
 0:28:23
0:28:23
 0:10:35
0:10:35