filmov
tv
The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever?

Показать описание
In this video, we take a look at one of the most beautiful algorithms ever created: the Fast Fourier Transform (FFT). This is a tricky algorithm to understand so we take a look at it in a context that we are all familiar with: polynomial multiplication. You will see how the core ideas of the FFT can be "discovered" through asking the right questions. The key insights that are presented in this video is that polynomial multiplication can be improved significantly by multiplying polynomials in a special value representation. The challenge that presents itself is the problem of converting a polynomial from a standard coefficient representation to value representation.
We see that the FFT is an incredibly efficient recursive algorithm that performs this task, and we also discover that a slightly tweaked FFT (Inverse FFT) can also solve the reverse problem of interpolation. If this video doesn't blow your mind, I don't know what will.
0:00 Introduction
2:19 Polynomial Multiplication
3:36 Polynomial Representation
6:06 Value Representation Advantages
7:07 Polynomial Multiplication Flowchart
8:04 Polynomial Evaluation
13:49 Which Evaluation Points?
16:30 Why Nth Roots of Unity?
18:28 FFT Implementation
22:47 Interpolation and Inverse FFT
26:49 Recap
Also a subtle mistake that a commenter made me aware of -- at 26:40 instead of replacing w with (1/n * e^{-2 * pi i/ n}), the actual right way to do this is by taking the final output of the IFFT at the end of the recursion and dividing by n.
So the full change is w = e^{-2 pi i / n}
And then somewhere outside the scope of the IFFT function ifft_result = 1/n * IFFT(values)
The treatment of the FFT in this video is inspired by several well known references, mainly Introduction to Algorithms (Cormen et al.) and Algorithms (Papadimitriou et al.).
Music:
All other music by Aakash Gandhi
SVG Attributions:
We see that the FFT is an incredibly efficient recursive algorithm that performs this task, and we also discover that a slightly tweaked FFT (Inverse FFT) can also solve the reverse problem of interpolation. If this video doesn't blow your mind, I don't know what will.
0:00 Introduction
2:19 Polynomial Multiplication
3:36 Polynomial Representation
6:06 Value Representation Advantages
7:07 Polynomial Multiplication Flowchart
8:04 Polynomial Evaluation
13:49 Which Evaluation Points?
16:30 Why Nth Roots of Unity?
18:28 FFT Implementation
22:47 Interpolation and Inverse FFT
26:49 Recap
Also a subtle mistake that a commenter made me aware of -- at 26:40 instead of replacing w with (1/n * e^{-2 * pi i/ n}), the actual right way to do this is by taking the final output of the IFFT at the end of the recursion and dividing by n.
So the full change is w = e^{-2 pi i / n}
And then somewhere outside the scope of the IFFT function ifft_result = 1/n * IFFT(values)
The treatment of the FFT in this video is inspired by several well known references, mainly Introduction to Algorithms (Cormen et al.) and Algorithms (Papadimitriou et al.).
Music:
All other music by Aakash Gandhi
SVG Attributions:
Комментарии
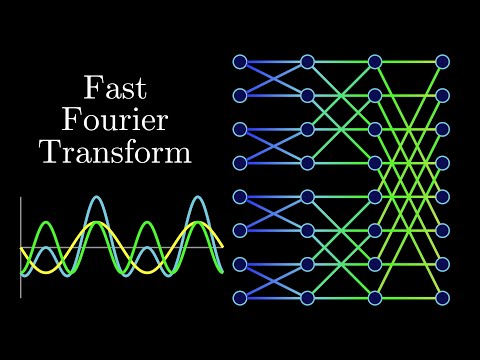 0:28:23
0:28:23
 0:08:46
0:08:46
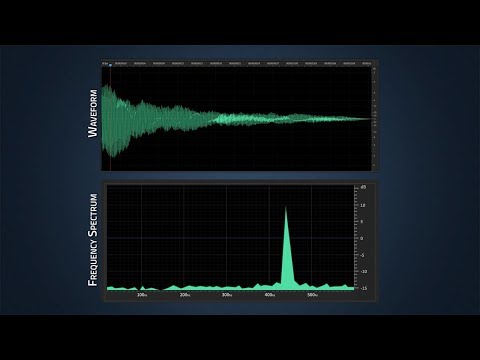 0:01:48
0:01:48
 0:19:20
0:19:20
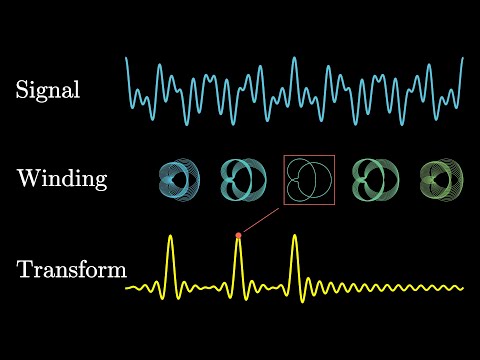 0:20:57
0:20:57
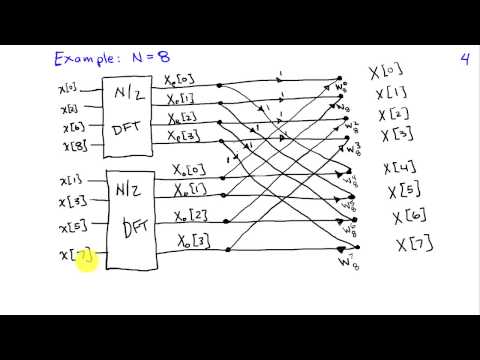 0:18:55
0:18:55
 0:10:18
0:10:18
 0:10:05
0:10:05
 0:07:27
0:07:27
 1:20:52
1:20:52
 0:01:32
0:01:32
 0:20:27
0:20:27
 0:19:08
0:19:08
 0:12:11
0:12:11
 0:19:19
0:19:19
 0:13:27
0:13:27
 0:10:35
0:10:35
 0:13:37
0:13:37
 0:10:47
0:10:47
 0:29:24
0:29:24
 0:07:39
0:07:39
 0:14:48
0:14:48
 0:07:28
0:07:28
 0:17:36
0:17:36