filmov
tv
Can you find area of circle? | (Fun Geometry Problem) | #math #maths | #geometry
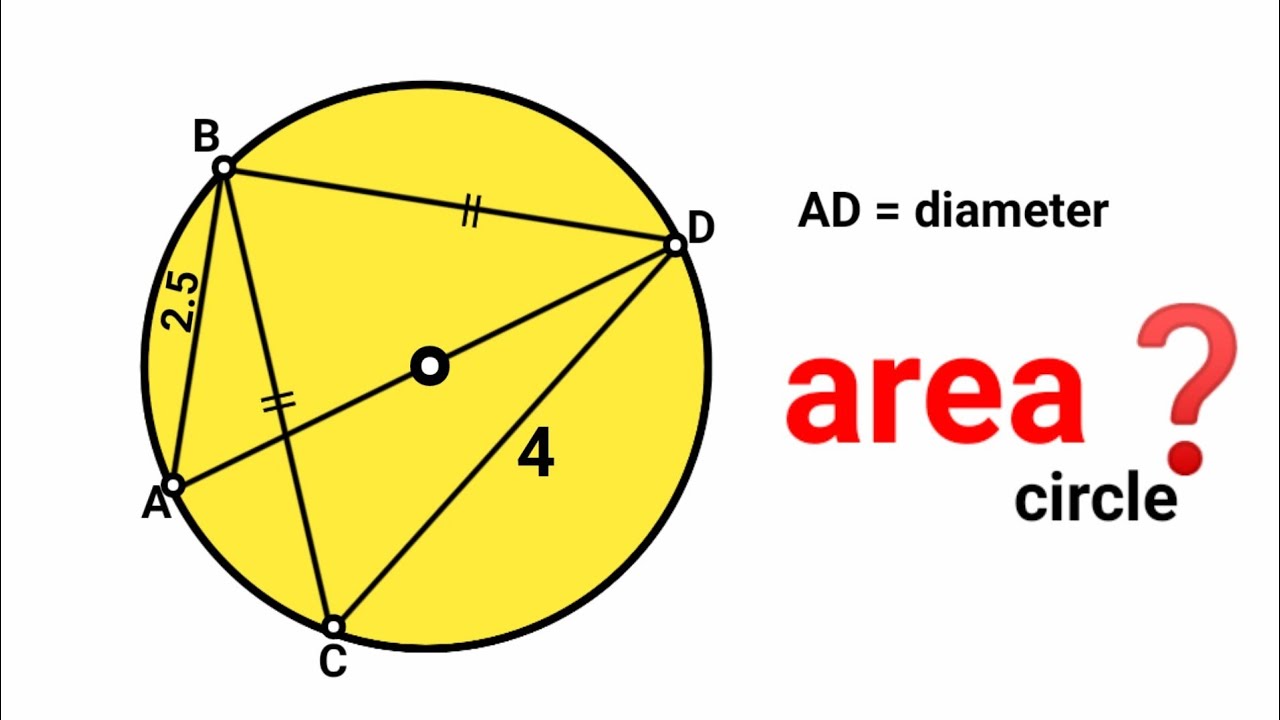
Показать описание
Find the Area Challenge
Can you calculate area of the Blue Parallelogram? | (Rectangle) | #math #maths | #geometry
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
Can YOU find the area? – Math problem
Can you find the red area? – Geometry puzzle
Can you find area of the Triangle? | (Find Side lengths) | #math #maths | #geometry
How to Find the Area of a Rectangle | Math with Mr. J
Can you find area of the Purple shaded Trapezoid? | (Right Triangles) | #math #maths | #geometry
Geometry Challenge: Find the Area & Number of Triangles! 🧮✨ #GCSEMaths #MathChallenge
Can you find area of the Blue shaded region? | (Think outside the Box) | #math #maths | #geometry
Can you find Area of the triangle? | (Algebra) | #math #maths | #geometry
Can you find area of the Green shaded triangle? | (QuarterCircle) | #math #maths | #geometry
Find the Area of an Equilateral Triangle
Can you find Area of the Green triangle? | (Olympiad) | #math #maths | #geometry
Area of rectangle | How to find area of a rectangle #shorts
Can you find area of the six Yellow shaded Squares? | (Rectangle) | #math #maths | #geometry
Can you find area of the Green shaded region? | (Circles) | #math #maths | #geometry
Can you find area of the Purple and Green Triangles? | (Justify) | #math #maths | #geometry
Can you find area of the Green shaded region? | (Squares) | #math #maths | #geometry
Can you find area of the Rectangle? | (Justify your answer) | #math #maths | #geometry
Can you find the Area of the Green Shaded Region? | 2 Simple Methods
Can you find area of the Green shaded rectangle? | (3 Methods) | #math #maths | #geometry
Can you find area of the Purple Square? | (Triangle) | #math #maths | #geometry
Find Area of Triangle | #shorts #shortvideo #viral #trending #mathsshorts
Комментарии
 0:04:33
0:04:33
 0:08:31
0:08:31
 0:22:10
0:22:10
 0:05:18
0:05:18
 0:06:27
0:06:27
 0:08:02
0:08:02
 0:04:43
0:04:43
 0:12:38
0:12:38
 0:00:55
0:00:55
 0:05:35
0:05:35
 0:08:04
0:08:04
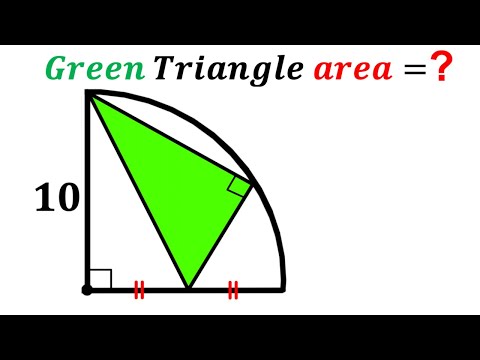 0:09:56
0:09:56
 0:00:47
0:00:47
 0:09:01
0:09:01
 0:00:30
0:00:30
 0:10:55
0:10:55
 0:12:03
0:12:03
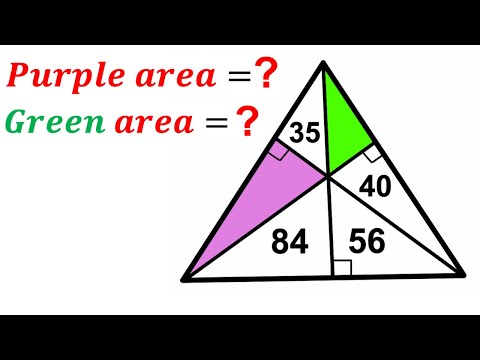 0:11:27
0:11:27
 0:12:35
0:12:35
 0:10:00
0:10:00
 0:10:49
0:10:49
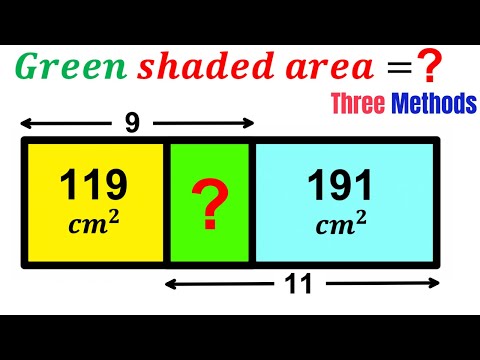 0:12:49
0:12:49
 0:11:38
0:11:38
 0:00:10
0:00:10