filmov
tv
Relative and Absolute Maximums and Minimums | Part II
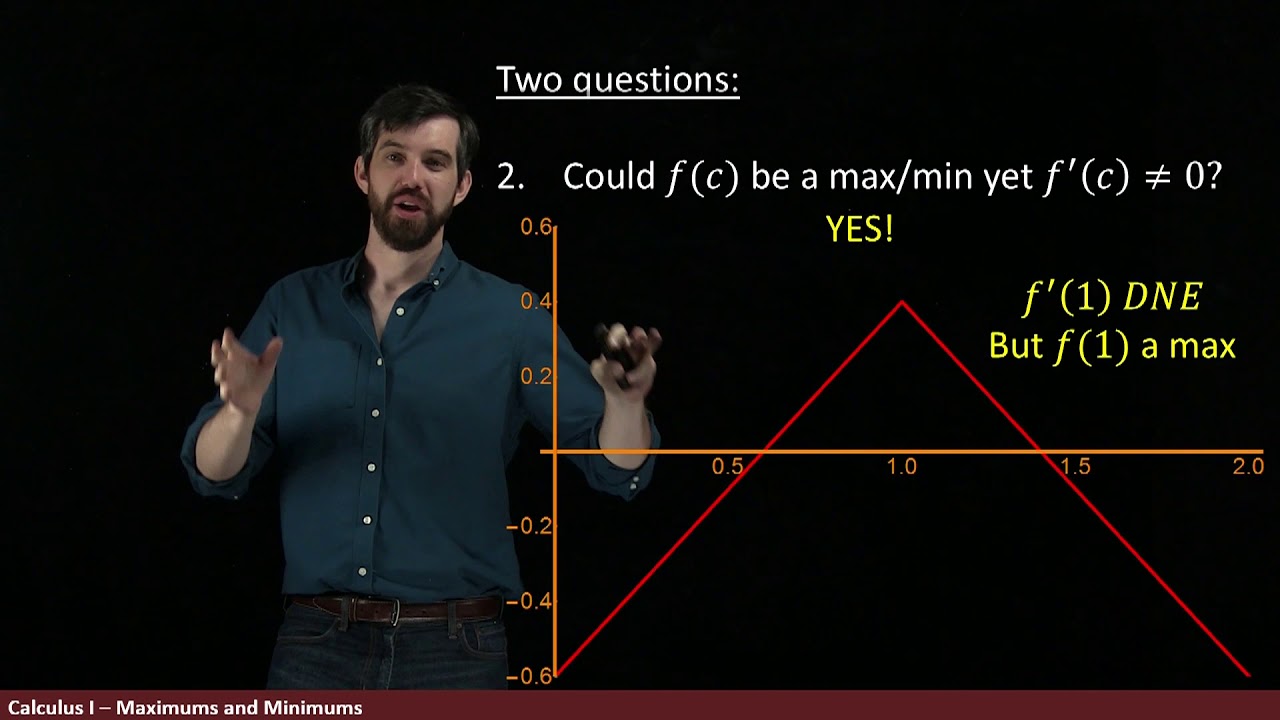
Показать описание
Learning Objectives:
1) Define Critical Points
2) For a function, compute the critical points
3) Construct examples of functions with and without extrema
Now it's your turn:
1) Summarize the big idea of this video in your own words
2) Write down anything you are unsure about to think about later
3) What questions for the future do you have? Where are we going with this content?
4) Can you come up with your own sample test problem on this material? Solve it!
Learning mathematics is best done by actually DOING mathematics. A video like this can only ever be a starting point. I might show you the basic ideas, definitions, formulas, and examples, but to truly master calculus means that you have to spend time - a lot of time! - sitting down and trying problems yourself, asking questions, and thinking about mathematics. So before you go on to the next video, pause and go THINK.
This video is part of a Calculus course taught by Dr. Trefor Bazett at the University of Cincinnati.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
1) Define Critical Points
2) For a function, compute the critical points
3) Construct examples of functions with and without extrema
Now it's your turn:
1) Summarize the big idea of this video in your own words
2) Write down anything you are unsure about to think about later
3) What questions for the future do you have? Where are we going with this content?
4) Can you come up with your own sample test problem on this material? Solve it!
Learning mathematics is best done by actually DOING mathematics. A video like this can only ever be a starting point. I might show you the basic ideas, definitions, formulas, and examples, but to truly master calculus means that you have to spend time - a lot of time! - sitting down and trying problems yourself, asking questions, and thinking about mathematics. So before you go on to the next video, pause and go THINK.
This video is part of a Calculus course taught by Dr. Trefor Bazett at the University of Cincinnati.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Learn how to find the absolute max, min and relative max min of a graph
How to recognize relative and absolute maxima and minima | Functions | Algebra I | Khan Academy
Identifying The Relative Maximum and Minimum Values of a Function
📈 Local and Absolute Maximum and Minimum from a Graph 📈
Relative and Absolute Maximums and Minimums | Part I
Finding Absolute Maximum and Minimum Values - Absolute Extrema
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
Relative and Absolute Maximums and Minimums | Part II
Taking it to the max: optimization problems
Finding Local Maximum and Minimum Values of a Function - Relative Extrema
Introduction to Absolute Vs Relative Maximums and Minimums
Absolute and Relative Extrema From a Graph Explained Intuitively
Introduction to minimum and maximum points | Functions | Algebra I | Khan Academy
How to Find the Absolute Maximum, Absolute Minimum, Relative Maximum,Relative Minimum from the Graph
Finding Local Maxima and Minima by Differentiation
Relative and Absolute Maximum/Minimum Values
Absolute and Relative Extrema (conceptual)
Absolute and Relative Extrema Introduction
Introduction to relative and absolute extrema of functions
Absolute Maximum and Minimum Values of Multivariable Functions (Part 1)
Absolute and Relative Extrema From a Graph (Open Interval)
Relative and Absolute Extrema
Relative and absolute maximum and minimum IB AI SL Calculus
🔶15 - Absolute (Global) and Relative (Local) Maximum and Minimum Values of a Function
Комментарии
 0:02:41
0:02:41
 0:04:58
0:04:58
 0:03:47
0:03:47
 0:03:27
0:03:27
 0:04:38
0:04:38
 0:17:17
0:17:17
 0:11:24
0:11:24
 0:07:23
0:07:23
 1:01:41
1:01:41
 0:14:18
0:14:18
 0:06:58
0:06:58
 0:01:54
0:01:54
 0:05:30
0:05:30
 0:01:41
0:01:41
 0:06:17
0:06:17
 0:05:21
0:05:21
 0:01:43
0:01:43
 0:02:00
0:02:00
 0:13:25
0:13:25
 0:06:18
0:06:18
 0:04:00
0:04:00
 0:09:47
0:09:47
 0:06:25
0:06:25
 0:19:17
0:19:17