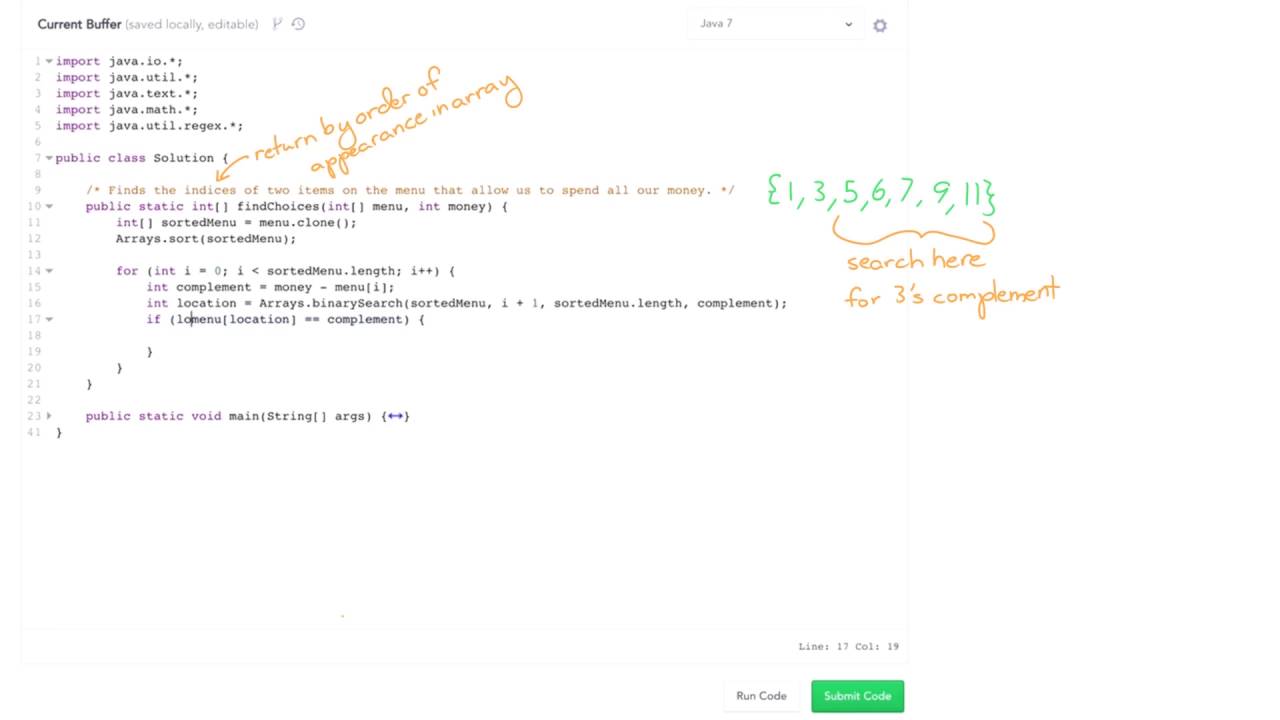
Algorithms: Solve 'Ice Cream Parlor' Using Binary Search

Learn how to solve the 'Ice Cream Parlor' using binary search algorithm. This video is a part of HackerRank's Cracking The Coding Interview Tutorial with Gayle Laakmann McDowell.

[aswinbeats]

Spent a lot of time trying to figure out why she used menu[i] within the loop. Should have watched the whole video first! If anyone is confused just like I was, don't worry. It's a typo. It's actually sortedMenu[i]

[George-nxzu]

I actually liked the idea of a struct/class to represent the menu item and its index. It requires more memory but I just like the idea of a MenuItem being able to remember its original index no matter what sorting algorithm is chosen.

[AmanSharma-hifd]

Why not just use meet in the middle approach to solve? That will be just O(n) rather than O(nlogn).
P.S : The complexity of the entire solution will still be O(nlogn) due to sorting.

[TRANTuanHiep]

This solution have a flaw, when the prices of 3 different creams are the same, the indexOf always return two first index and the solution for the third cream is never included

[haggailiu]

You could make indexOf take 2 values v1, v2. Then search in opposite directions and return an int array of length 2

[infinite]

A simple way to approach this problem would be the following:

Treat the ice cream list as an array of integers

Treat the money the person has as the target score

Sort the ice cream array in ascending order (lowest - highest priced)

Create a variable that will mark the beginning of the array.

Create a variable that will mark the end of the array.

Add both elements and make the following decisions based on the comparisons:

If the sum is equal to the target then return the value stored in both markers

Else if sum is less than target then move the left marker to the right by one

Else If sum is greater than target then the target move the right marker to the left by one.

Loop until you find a pair that adds up to the target

I believe this would be an O(n) algorithm since there is a possibility we will compare all items in the array

However the space complexity is constant since there is no need for external storage aid

[zeta.x]

To the people who are asking why she would prefer a more complex answer vs the O(n) time and space hash table solution, there are times in an interview where:
1. They will give you a space constraint, or
2. They will ask for alternative solutions to test your knowledge

Admittedly it's confusing that she did a 'clone' on the array since that's the same space complexity as the hash solution, but I've been in interviews where (minus the array clone) this is basically the solution they were looking for, because it optimizes on space.
Many times the "correct solution" an interviewer is looking for will do a tradeoff on time to optimize on space.

[ananamz]

Please correct me if I am wrong. The complexity of the following is O(n2) because "in" has a complexity of O(n) and we are going to through each item in the array once which is O(n)?


arr = [2, 7, 13, 5, 4, 13, 5, 9, 1]

target_amount_to_spend = 10
indices = []
for i in range(len(arr)):
if (10-arr[i])in arr:
indices.append(i)
print("Present")

print(indices)

[dmitryWeirdo]

This actually has an additional complexity for sorting an array (Java's Arrays.sort will be quicksort complexity, so it is O(n * log N ) ) and this straightforward bruteforce way of searching for indices adds 2 * n complexity. And, finally, binary search O(log N) complexity is added.

So the solution with a HashMap which is O(n) is much, much better. No reason to use binary search for this task.
I immediately wrote a HashMap solution and still do not understand what is the win of binary search here.

[bennyyeung]

This one is easy to follow, but still takes time to digest

[arpit]

The code is great and easy after watching this video. But it was very tough to come up with when trying to solve the problem!

[notramiras]

I don't get why sorting is needed at all. Go through all the elements, and push them in a hashmap where the key is the expected complement value, and the value is the index. The first time you encounter an item for which the complement exists in the hash, you have the result. Worst case O(N), best case O(1). What am I missing?

[antoniofontaine]

Dont know why she creates two functions to get the indexes... when they are i and location right? We also know the order of appearance, i goes first and then location. Line 33, could be replaced with: int[] indices = { i, location};

[yadhumoore]

Four (not including function name) lines in Python:
def findChoices(menu, money):
for i in menu:
if money - menu[i] in menu[i+1:]:
return i, menu.index(money - menu[i], i+1, len(menu))
return None

[arashkeyghobadi]

My solution in JavaScript:

function icecreamParlor(m, arr) {

let length = arr.length;
let stack = [];

for(let i = 0; i < length; i++) {

let price = arr[i];

if(price >= m)
continue;

for(let j of stack) {
if(j.moneyLeft - price === 0)
return [(j.index + 1), (i + 1)];
}

stack.push({
index: i,
moneyLeft: m - price
});

}

}

[ayushranjan]

Why do we need to binary search for each element in the array when there is a more efficient solution possible. The current solution has a sort so O(n logn) and then we do worst case n binary searches which is again O(n logn). Instead what we can do is after sorting has an end pointer and start pointer. If the sum is greater than required then increment start pointer, if lesser decrement end pointer and if equal we have our answer. This is O(n). I know this does not affect the Big-O runtime but this surely is faster.

[aslemisaac]

how about sorting and solving it using two pointers..to meet in the middle

[OnLifeandLove]

Why didn't she just search for the complement in the original menu? That would be O(n) and less complicated

[aleramos]

This solutions it dosn't work in c#, ends with "Runtime Error". If someone get to a working solution please post the code. Thanks!

[Eliecerhdz]

Isnt the sorting of the array an O(n)?