Trigonometry Proof: cos (x + y) = cos x cos y – sin x sin y (https://youtu.be/b0o_dvFkYbU)

Trigonometry Proof: cos (x + y) = cos x cos y – sin x sin y

MANY MORE ARE THERE IN THE PLAYLIST. PLEASE PLEASE CHECK ONCE. YOU WILL BE AMAZED TO SEE THE QUESTIONS.

In all these videos on Trigonometric Functions I have always focused on explaining the basics and then solving the questions. My way of solving question will always refer back to the basics explained previously so that students can make the connect between basics and application of them.

Lets start:
Arc/ Angle and Radian
Relation between Degree and Radian
Radian measure/ Degree measure
If x increase or decreases by the integral multiple of 2\mathbit{\pi}, the value of sine or cosine functions do not change
sin(2n\mathbit{\pi} + x) = sinx , n \in Z
cos(2n\mathbit{\pi} + x) = cosx , n \in Z cos x = 0, if x = 0, \pm\mathbit{\pi}/2, \pm\mathbf{3}\mathbit{\pi}/2, \pm\mathbf{5}\mathbit{\pi}/2,……i.e.., when x is an odd multiple of \mathbit{\pi}/2 .
cos x = 0 implies x = (2n + 1) \frac{\mathbit{\pi}}{\mathbf{2}}, where n is an integer
sin x = 0, if x = 0, \pm\mathbit{\pi}, \pm\mathbf{2}\mathbit{\pi}, \pm\mathbf{3}\mathbit{\pi},……i.e.., when x is an integral multiple of \mathbit{\pi} .
Sin x = 0 implies x = n\mathbit{\pi}, where n is an integer
Sign of Trigonometric Functions
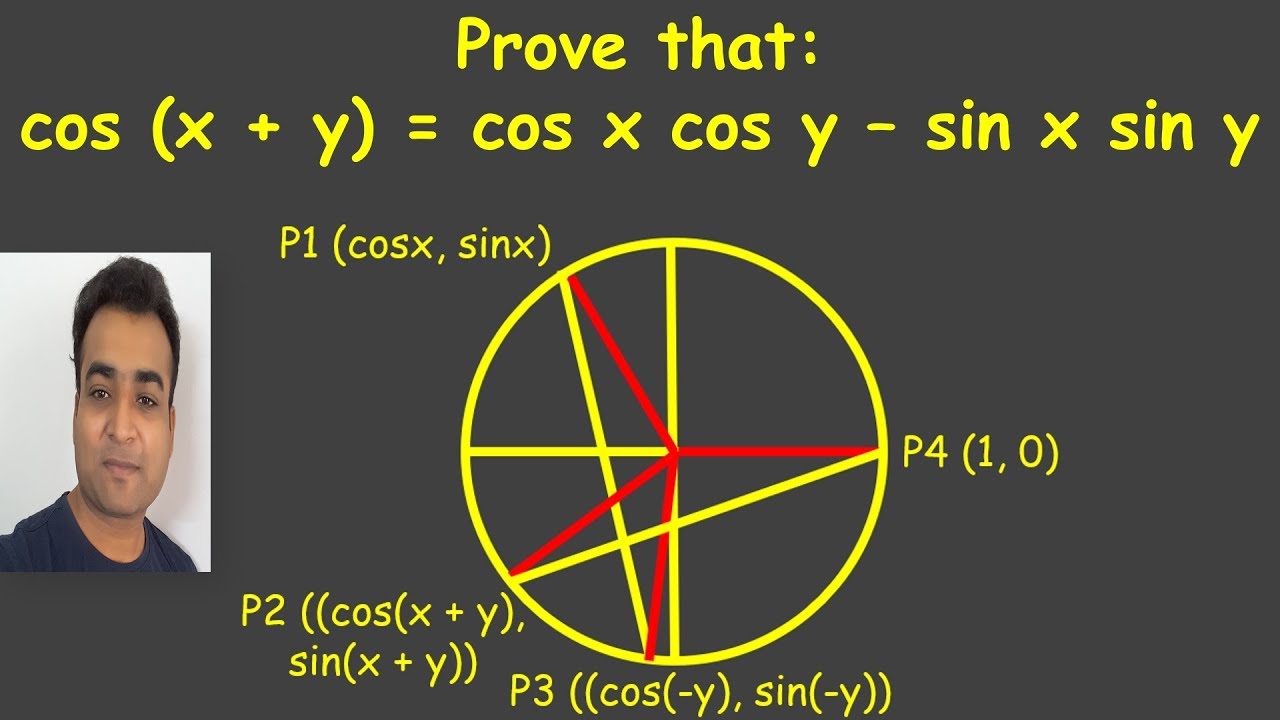
Cos (x + y) = cos x cos y – sin x sin y
Principal Solutions
General Solutions
Principal Solutions:
Given x value has solutions which are less than 2\mathbit{\pi} and more than or equal to 0, those solutions are called principal solutions:

Sets, Relations and Functions, Trigonometric Functions, Permutations and Combinations, Linear Inequality, Binomial Theorem, Straight Lines, Conic Sections.

Find us on youtube

Find us on Facebook:
Contact:
Abhishek Agarwaal
[phone]

Cos (x + y) = cos x cos y – sin x sin y

Mathsphy

[mspseducation]

Just wanted to know why triangles were considered congruent! It was so simple I realized after ur explanation. Thanks :)

[janvisagie]

This is how the proof should be done properly...Thank you kind sir.

[ganeshkhanapur]

Thank you so much sir for understanding this. I didn't understanding from book after watching this video I I completely understood.

[AzanOggy]

Thank u so much sir I didn’t understand I studied in English medium school but now I’m studying in government college, they are teaching in Kannada language now I understand perfectly once again thank u soooo much ❤❤❤❤

[khalilzidane]

Sir but distance formula is (x2-x1)^2 + (y2-y1)^2
By this we get
[cos(-y)-cos(x)] + [sin(-y) - sin(y)]
How this is equal to ur method??

[problemsolver]

Thankyou Sir
Now I understood this concept perfectly ☺️

[dhanwantariprajapati]

Sir can you pls explain why the coordinates of p2 are [cos(x+y), sin(x+y)]

[lakshmitha_]

I wish you were my maths teacher, thank you sir you have made this so simple for me

[nehaka]

Thank you so much sir😊😊 you gave me complete concept clarity🙏🏻☺️

[sameermujawar]

Thank you so much sir for understanding

[Princeprakashdz]

You help as god to those who is not able To go next .
Anyway you explanation didno need of arise question in student silent mind

[raninekkanti]

Ur explanation helped me lot sir thank you:)

[pareshgandhi]

Sir I have a doubt that


You proved the coordinates to be taken as ( cosx, sinx ) for the angle which was taken was acute

But

How can say the same thing for an obtuse angle..???

Please help me to solve my doubt...

[stunterboy]

Sir it was very helpful at last moment thank you sir I understood it very quickly 🙏🙏

[sanjivkumar-nxhq]

Sir in third quadrant the value of x and y is neg then why we wrote
[Cos-cos(-y)]sq = (cos-cosy)sq.
And sir if it is right then why didn't we write in second equation

[siddharthdhaka]

Sir first quad and 2nd k cordinate same ho gye (cosx sinx)1:57 pe

[entropy]

TO THOSE WHO DID NOT GET IT. pls go for a quick recap of the distant formula which u have learned in cl10

[huligemmakhuligemmak]

Tq sir it's easy to remember tq so much dir

[dr.sabhambbs]

Sir u actually didn't explain we have to use distance formula and didn't prove the triangles are congruent

[afreenbanu]

in P2P4 why did u have added +1 at last in 3 step