filmov
tv
Expand & Simplify: (x + 1)^3
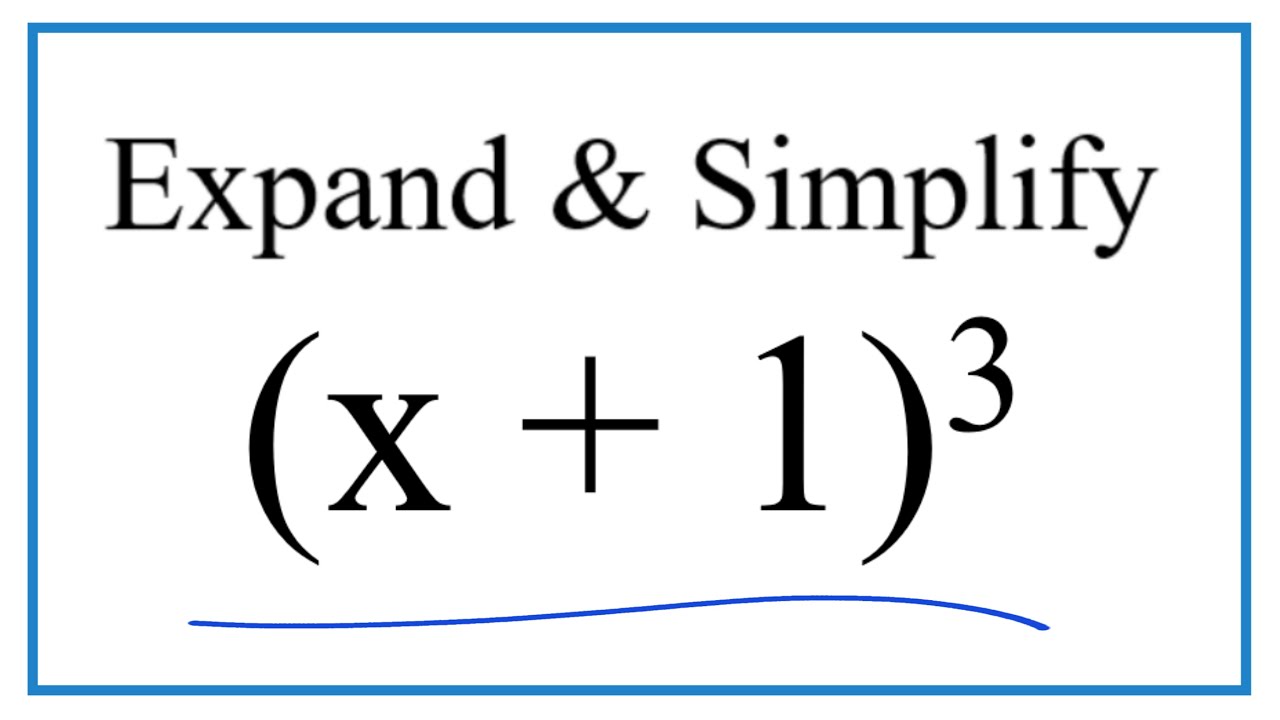
Показать описание
In this video we will solve, expand and simplify (x + 1)^3 we can think of this as (x + 1)(x + 1)(x + 1).
It works best to multiple (x + 1)(x + 1) first and then multiply that expression by (x + 1).
When we multiply (x + 1)(x + 1) we get:
x2 + 2x + 1
We then multiply that by (x + 1):
(x+1)(x2 + 2x + 1)
using the distributive property.
After we add like terms we end up with:
x3 + 3x2 + 3x + 1
Often the FOIL method is used to help students remember (but it's the same thing as described above). We multiply the first terms, then the outside terms, the inside terms and finally the last terms.
F ("first" terms of each binomial are multiplied together)
O ("outside" terms are multiplied: the first term of the 1st binomial and the 2nd term of the second)
I ("inside" terms are multiplied—second term of the first binomial and first term of the second)
L ("last" terms of each binomial are multiplied)
Expanding algebraic expressions is a key skill in mathematics.
It works best to multiple (x + 1)(x + 1) first and then multiply that expression by (x + 1).
When we multiply (x + 1)(x + 1) we get:
x2 + 2x + 1
We then multiply that by (x + 1):
(x+1)(x2 + 2x + 1)
using the distributive property.
After we add like terms we end up with:
x3 + 3x2 + 3x + 1
Often the FOIL method is used to help students remember (but it's the same thing as described above). We multiply the first terms, then the outside terms, the inside terms and finally the last terms.
F ("first" terms of each binomial are multiplied together)
O ("outside" terms are multiplied: the first term of the 1st binomial and the 2nd term of the second)
I ("inside" terms are multiplied—second term of the first binomial and first term of the second)
L ("last" terms of each binomial are multiplied)
Expanding algebraic expressions is a key skill in mathematics.
 0:01:37
0:01:37
 0:00:51
0:00:51
 0:00:44
0:00:44
 0:05:11
0:05:11
 0:00:19
0:00:19
 0:01:36
0:01:36
 0:08:19
0:08:19
 0:00:55
0:00:55
 0:01:38
0:01:38
 0:00:21
0:00:21
 0:22:51
0:22:51
 0:00:19
0:00:19
 0:03:07
0:03:07
 0:02:40
0:02:40
 0:01:35
0:01:35
 0:01:04
0:01:04
 0:01:11
0:01:11
 0:02:49
0:02:49
 0:00:25
0:00:25
 0:21:34
0:21:34
 0:01:03
0:01:03
 0:02:24
0:02:24
 0:01:08
0:01:08
 0:01:18
0:01:18