filmov
tv
Expand & Simplify: (x + 1)^2
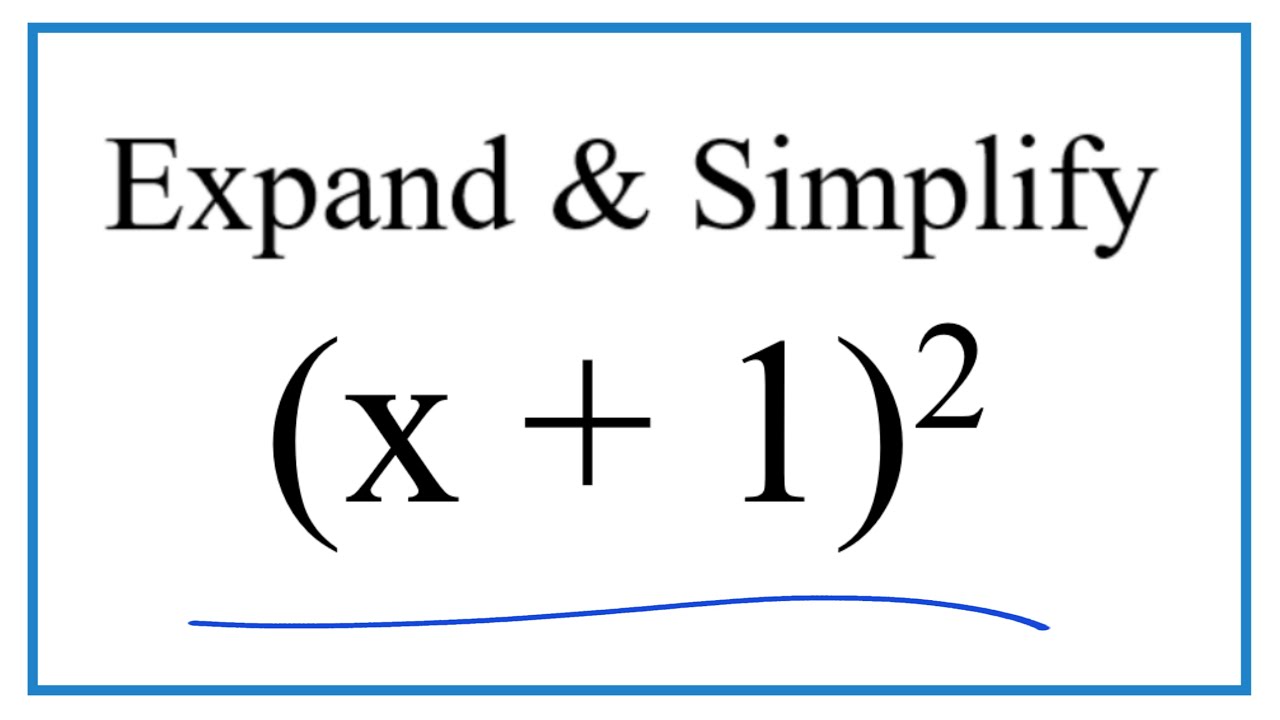
Показать описание
To expand and simplify (x + 1)^2 we can think of this as (x + 1)(x + 1). We then can first multiply x by (x + 1) and then multiply 1 by (x+1). After that we can combine any like terms to simplify. We are essentially using the distributive property to expand and simply (x + 1)(x + 1).
Often the FOIL method is used to help students remember (but it's the same thing as described above). We multiply the first terms, then the outside terms, the inside terms and finally the last terms.
F ("first" terms of each binomial are multiplied together)
O ("outside" terms are multiplied: the first term of the 1st binomial and the 2nd term of the second)
I ("inside" terms are multiplied—second term of the first binomial and first term of the second)
L ("last" terms of each binomial are multiplied)
For both methods we end up with:
x2 + x + x +12
which we can simplify to:
x2 + 2x + 1
If you were to factor x2 + 2x + 1 you'd get (x + 1)(x + 1) which could be written as:
(x+1)^2
Expanding algebraic expressions is a key skill in mathematics.
Often the FOIL method is used to help students remember (but it's the same thing as described above). We multiply the first terms, then the outside terms, the inside terms and finally the last terms.
F ("first" terms of each binomial are multiplied together)
O ("outside" terms are multiplied: the first term of the 1st binomial and the 2nd term of the second)
I ("inside" terms are multiplied—second term of the first binomial and first term of the second)
L ("last" terms of each binomial are multiplied)
For both methods we end up with:
x2 + x + x +12
which we can simplify to:
x2 + 2x + 1
If you were to factor x2 + 2x + 1 you'd get (x + 1)(x + 1) which could be written as:
(x+1)^2
Expanding algebraic expressions is a key skill in mathematics.
(x+3)(x+5) Expand and Simplify
Expanding & Simplifying Single Brackets - Tutorial / Revision
Expand and simplify (2a+3)(3a-4)
(x-3)(x+3) Simplify | Expand and Simplify a product of algebraic expressions
(x+2)(x+3) Expand and Simplify
4(x+3) - 3(x+2) Expand and Simplify
E𝒙𝒑𝒂𝒏𝒅 and Simplify 𝒙 (𝒙+𝟏)(𝒙+𝟐)
Expand & Simplify: (x + 1)(x + 1)
Ma5, Solutions to Homework 5 Problems
(x+a)(x+b)(x+c) Expand and Simplify
Expand & Simplify: (x + 1)^2
Expand & Simplify: (x + 2)(x + 1)
Expand & Simplify: (x + 1)(x + 3)
Expand and simplify terms in brackets - 3 minute maths
Expand & Simplify: (x + 2)(x + 3)
Expand & Simplify: (x - 1)(x - 2)
Simplify (x-4)^2 || Expand and simplify x-4 square
(x+2)^2 expand and simplify using FOIL method
Expand & Simplify: (x - 1)(x - 2)
Expand & Simplify: (x + 3)^2
How to expand and simplify (x+1)(2x+1) binomials
Expand & Simplify: (x - 1)^2
Expand & Simplify: (x - 2)(x - 3)
Expand & Simplify: (x - 1)(x - 1)
Комментарии
 0:00:44
0:00:44
 0:05:11
0:05:11
 0:00:55
0:00:55
 0:01:02
0:01:02
 0:01:18
0:01:18
 0:00:42
0:00:42
 0:01:35
0:01:35
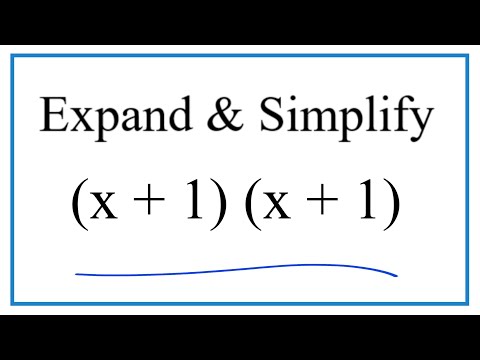 0:01:04
0:01:04
 0:24:10
0:24:10
 0:03:41
0:03:41
 0:01:36
0:01:36
 0:01:37
0:01:37
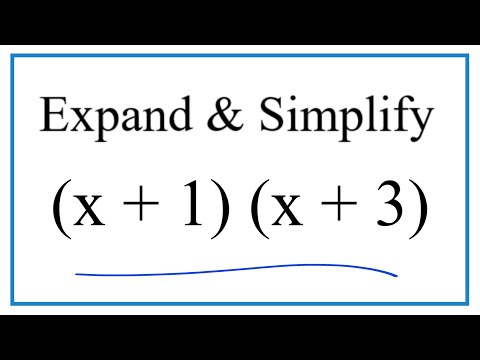 0:01:02
0:01:02
 0:02:53
0:02:53
 0:01:04
0:01:04
 0:01:11
0:01:11
 0:01:06
0:01:06
 0:01:14
0:01:14
 0:01:08
0:01:08
 0:01:19
0:01:19
 0:02:17
0:02:17
 0:01:38
0:01:38
 0:01:03
0:01:03
 0:01:08
0:01:08