filmov
tv
Calculus 3: Divergence and Curl (23 of 32) The Laplace Operator: Ex. 1
Показать описание
In this video I will find the Laplace operator of f=x^2+y^3+x(y^2)z.
Next video in the series can be seen at:
0:15:42
Divergence and curl: The language of Maxwell's equations, fluid flow, and more
0:13:11
Divergence and Curl (Vector Fields)
0:15:36
Vector Fields, Divergence, and Curl
1:11:50
Calculus 3 Lecture 15.2: How to Find Divergence and Curl of Vector Fields
0:31:46
16.5: Curl & Divergence
0:07:06
Calculus 3: Divergence and Curl (3 of 26) What is the Divergence?
0:13:02
Div, Grad, and Curl: Vector Calculus Building Blocks for PDEs [Divergence, Gradient, and Curl]
0:36:47
Calculus 3: Curl and Divergence (Video #31) | Math with Professor V
0:03:42
Calculus 3: Divergence and Curl (1 of 26) What is the Del Operator?
0:08:23
Calculus 3: Divergence and Curl (2 of 26) What is the Gradient?
0:12:21
curl and divergence (KristaKingMath)
0:08:18
A unified view of Vector Calculus (Stoke's Theorem, Divergence Theorem & Green's Theor...
0:04:40
Calculus 3: Divergence and Curl (7 of 32) What is the Divergence? A Visual Solution
0:02:25
Calculus 3: Divergence and Curl (11 of 50) Calculating the Divergence (Cartesian) Ex. 4
0:06:50
Calculus 3: Divergence and Curl (32 of 50) An Interesting Example
0:06:27
Calculus 3: Divergence and Curl (31 of 50) Identity 7: CURL[CURL(F)]=Grad[DIV(f)] – (Grad)^2(F)
0:08:26
The CURL of a 3D vector field // Vector Calculus
0:10:40
Calculus 3: Divergence and Curl (28 of 50) Identity 4: CURL(f G)=f [CURL(F)]+Gradient(f)xF
0:05:25
Calculus 3: Divergence and Curl (25 of 50) Identity 1: DIV(F+G)=DIV(F)+DIV(G)
0:02:44
Calculus 3: Divergence and Curl (34 of 50) Cylindrical Coordinates: Small Displacement dr
0:06:43
Calculus 3: Divergence and Curl (27 of 50) Identity 3: DIV(f G)=f [DIV(F)]+F [Gradient(f)]
0:08:07
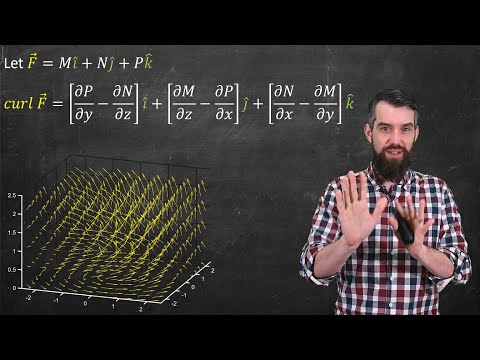
Calculus 3: Divergence and Curl (12 of 32) What is the Curl? Part 1
0:04:29
Calculus 3: Divergence and Curl (4 of 32) What is the Divergence? Part 2
0:02:25
Calculus 3: Divergence and Curl (10 of 50) Calculating the Divergence (Cartesian) Ex. 3
Комментарии