filmov
tv
Solve a Graph theory problem using Topology | Bruijn Erdos Theorem

Показать описание
Bruijn Erdos Theorem states thats if any subgraph of an infinite graph is k colorable, the graph itself is k colorable. Tychonoff's theorem can help us in proving the theorem which states that an arbitrary product of compact sets is compact.
How To Solve A Crime With Graph Theory
This number theory problem can be solved using graph theory
Introduction to Graph Theory: A Computer Science Perspective
Solve a Graph theory problem using Topology | Bruijn Erdos Theorem
How the Königsberg bridge problem changed mathematics - Dan Van der Vieren
Euler Paths & the 7 Bridges of Konigsberg | Graph Theory
The Chinese Postman Problem (Introduction to Graph Theory)
Dijkstras Shortest Path Algorithm Explained | With Example | Graph Theory
Matthew Akamatsu: 'Collective grassroots knowledge generation with lab discourse graphs'
Breadth First Search Algorithm | Shortest Path | Graph Theory
Explaining Components of Graphs | Graph Theory
Hamiltonian Cycles, Graphs, and Paths | Hamilton Cycles, Graph Theory
Solving the Königsberg Bridge Problem with Python | Graph Theory With Python #1
Breadth First Search grid shortest path | Graph Theory
Chinese Postman Problem || Chinese Postman Problem in Graph Theory
How to Master Graph Theory for Coding Interviews
Applications of Graph Colouring
Graph theory and triangular inequality come together - INMO 2023 Problem 5
ACSL Math: Graph Theory
Complement of a graph in graph theory | Theory and Numerical Problems
Graph Algorithms for Technical Interviews - Full Course
Overview of algorithms in Graph Theory
What are Vertex Disjoint Paths? | Graph Theory
Matchings, Perfect Matchings, Maximum Matchings, and More! | Independent Edge Sets, Graph Theory
Комментарии
 0:04:23
0:04:23
 0:09:52
0:09:52
 0:16:26
0:16:26
 0:02:34
0:02:34
 0:04:39
0:04:39
 0:06:24
0:06:24
 0:08:43
0:08:43
 0:08:24
0:08:24
 1:06:40
1:06:40
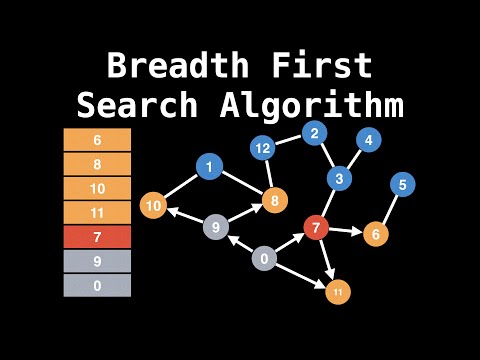 0:07:23
0:07:23
 0:08:05
0:08:05
 0:11:54
0:11:54
 0:32:02
0:32:02
 0:16:51
0:16:51
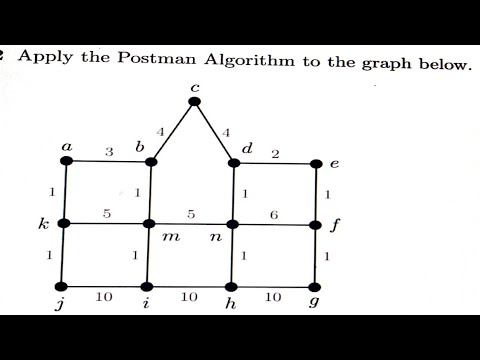 0:09:51
0:09:51
 0:08:03
0:08:03
 0:09:29
0:09:29
 0:30:15
0:30:15
 0:12:30
0:12:30
 0:15:44
0:15:44
 2:12:19
2:12:19
 0:09:47
0:09:47
 0:12:24
0:12:24
 0:18:01
0:18:01