filmov
tv
Euler Paths & the 7 Bridges of Konigsberg | Graph Theory

Показать описание
An Euler Path walks through a graph, going from vertex to vertex, hitting each edge exactly once. But only some types of graphs have these Euler Paths, it depends on the degree of the vertices. We state and motivate the big theorem, and then use it to solve the infamous 7 bridges of Konigsberg problem that motivated Euler to start studying graph theory.
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
Euler Paths & the 7 Bridges of Konigsberg | Graph Theory
Graph Theory: Euler Paths and Euler Circuits
Euler Paths and Circuits
Eulerian Path - Intro to Algorithms
Euler and non-Euler Paths & Circuits
Discrete Math II - 10.5.1 Euler Paths and Circuits
Euler Paths & Circuits
Euler Paths and Circuits Explained
Eulerian Path
Euler's Path
Existence of Eulerian Paths and Circuits | Graph Theory
Eulerian Path/Circuit algorithm (Hierholzer's algorithm) | Graph Theory
Level 7: Euler Circuits II From the Path Diagrams Math Program
Section 14.2, Video 7, Determining if a Graph has an Euler Path or an Euler Circuit
Euler Paths & Graph Theory
SAS 1 - Euler Paths & Circuits
Euler Paths And Circuits In Graph Theory - Part One
L2N2 - Euler Paths & Circuits
Euler and Hamiltonian paths and circuits
Königsberg Bridge Problem & Euler Path : Can You Draw A Graph Without Removing Pen From The Pape...
Euler and Hamilton Path: Cube Graph: Shortest Hamilton Path:
5.1 part 16: EX 7 Euler path or circuit
Ch 3.4.0: Euler and Hamilton Paths | Euler circuit & path | Graph Lectures by @MonalisaCS
Graph Theory Example: Existence of Euler Paths
Комментарии
 0:06:24
0:06:24
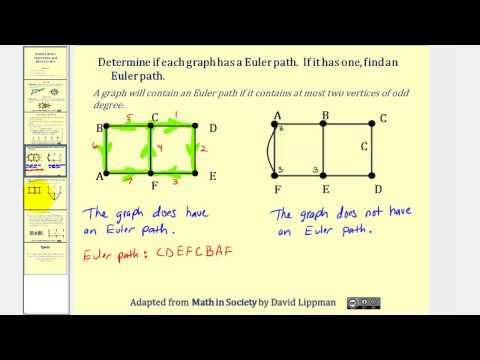 0:09:52
0:09:52
 0:09:44
0:09:44
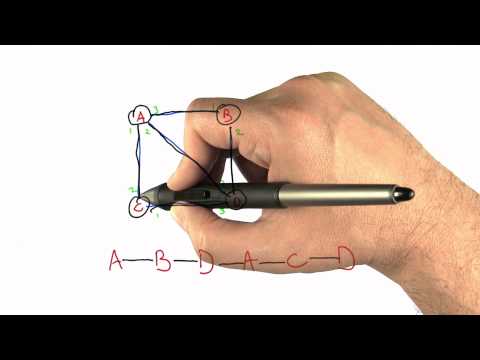 0:02:51
0:02:51
 0:05:08
0:05:08
 0:17:37
0:17:37
 0:13:58
0:13:58
 0:05:51
0:05:51
 0:02:32
0:02:32
 0:01:00
0:01:00
 0:09:41
0:09:41
 0:15:34
0:15:34
 0:00:22
0:00:22
 0:03:53
0:03:53
 0:02:51
0:02:51
 0:11:51
0:11:51
 0:04:17
0:04:17
 0:04:55
0:04:55
 0:10:18
0:10:18
 0:03:39
0:03:39
 0:00:25
0:00:25
 0:03:34
0:03:34
 0:09:17
0:09:17
 0:02:17
0:02:17