Solving the Königsberg Bridge Problem with Python | Graph Theory With Python #1

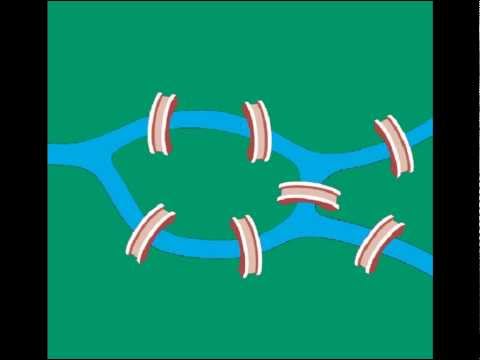
In this video, you'll see how to solve the famous Königsberg bridge problem from graph theory using pure Python. We'll write a recursive algorithm to check for eulerian circuits. Then we'l see how Euler solved the Königsberg bridge problem — which gave birth to the field of Graph Theory — and compare Euler's solution to the one we write in Python. Euler probably wouldn't like using Python to solve the problem!

TIMESTAMPS
¯¯¯¯¯¯¯¯¯¯¯¯¯¯
0:35 - What The Königsberg Bridge Problem Is
2:21 - How Euler Heard About the Problem
3:11 - How Leibniz Influence Euler to Attack the Problem
6:36 - How to Brute Force a Solution Using Python
19:38 - Why Euler Would Hate The Python Solution
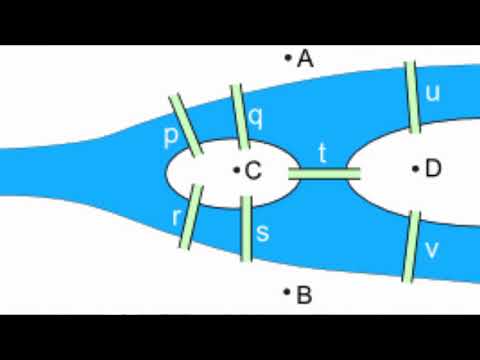
20:26 - How Euler Solved the Problem
29:20 - What Königsberg Has To Do With Graph Theory
31:11 - Final Thoughts and Conclusion

CODE REPOSITORY
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

GRAPH THEORY WITH PYTHON SERIES
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
➢ Part 1: YOU ARE HERE

HELPFUL LINKS
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
➢ The Truth About Königsberg by Brian Hopkins and Robin Wilson

➢ Analysis Situs, the Foundations of Mathematics, and a Geometry of Space by Vincenzo De Risi

➢ Itertools in Python 3, By Example

SUPPORT ME
¯¯¯¯¯¯¯¯¯¯¯¯¯
My content is, and always will be, completely free. But your support goes a long way to motivate me to continue to produce top-notch math and programming content. You can tip me using any of the following links:

OTHER LINKS
¯¯¯¯¯¯¯¯¯¯¯¯¯¯

#graphtheory #pythonprogramming #discretemath #discretemathematics

[mkartmkart]

Totally thumbsup with possibilities for more :) Thanx :)

[giannisgrammatikakis]

This is the channel I needed. Great job Danid! Thank you!

[samiakel]

Well done! Great explanation. I really enjoyed it

[JosephChan]

For another perspective on the Königsberg Bridge problem, one can consider the number of edges on each vertex.

To visit any vertex in a path once, there needs to be at least one edge going in, and another edge going out, for a total of 2 edges (so that each edge is only travelled once). If a vertex is visited twice, then there needs to be 2 edges in and 2 edges out, for a total of 4 edges. To generalise, any valid path needs an *even* number of edges for each edge to be visited once.

There are two exceptions: the start vertex and end vertex. For the start vertex, there doesn’t _need_ to be an edge in, only an edge out, so it can just have one edge. It’s possible that the start edge can be visited another time (in which case we need to add another pair of edges to go in and out). It’s also possible that in a cyclical graph (of say 3 nodes), the start vertex has an even number (2) of edges. Likewise, the end vertex doesn’t _need_ an edge out (although it can!).

From these facts, we can come up with a simple heuristic to solve this problem: there can be a maximum of 2 nodes with an odd number of edges. As the Königsberg graph has 3 vertices with an odd number of edges, it can’t be traversed with each edge being travelled only once.

[brightsideofmaths]

Great content, very good quality and really enjoyable. Thank you :)

[sinnvollerkommentar]

Very helpful if you want to get started in solving math problems yourself like I am. Also you showed very well how to include python

[CodeSolid]

I enjoyed this quite a bit. I thought the Python could have been a bit more "dumbed down" to be more approachable for others (since you clearly are quite good at it), but that's a minor quibble. I was able to follow it. I also enjoyed the historical details, as another poster mentioned.

[mukundraj]

Hi David.
Its a Theory + Explanation + Programming RIght Mix and Enjoyable Learning that I was looking for Research.

[VanessaHernandez-zdlg]

Very well done! I found the use of colors especially helpful since I’m a visual learner

[georgelaing]

This is the most complete treatment of the 7 bridge problem I have ever seen!
I especially enjoyed the historical details that you included.
You are right that Euler would have hated the work in
tabulating paths, although he did produce about 100 volumes of
work. Did they ever finish collecting his material?
Thanks again for a great video!

[avalealidzy]

Fully subscribed to channel. Your mathematical insights will have great applications to data science!

[slater-cguy]

Just discovering this channel, great content/presentation!

[yatima]

I was playing around with the walks_starting_from function and I think there is a bug. I wanted to get all walks from the 5 cycle encoded as C_5 = [ ‘AbB', 'BbC', 'CcD', 'DdE', 'EeA'], walks_starting_from(‘B’, C_5) gave [‘BbA’] where I would expect the answer is [‘BbAeEdDcC’, ‘BbCcDdEeA’] - going round the clock both clockwise and anticlockwise. Seems like you’re missing some walks and need more conditional logic somewhere.

Thanks for the great lecture otherwise! Look forward to learning more about how to implement graph theory.

[canaldofetrentin]

hii, I am taking a graph course in my university and from now on I'm watching your videos to get along with python etc. I just would like to know why is it necessary to declare a variable in available_bridhes and iterate over it, like:

available_bridges = [
bridge
for bridge in bridges:
]

not simply: available_bridges = [
for bridge in bridges
]

[avalealidzy]

Could this be considered a Search Optimization Algorithm?

[philipwest]

Euler (a Swiss-German gentleman) is pronounced more like eo-ler than it is like oi-ler. The English language doesn't really have a diphthong that matches the eu in Euler. Oi is an approximation but not a good one. Better would be a short soft o-ler. This is a slightly random comment 🙂