ГЛАВНАЯ ЗАДАЧА 9 КЛАССА! 5 или не 5? Вот в чем вопрос ... (Шекспир)

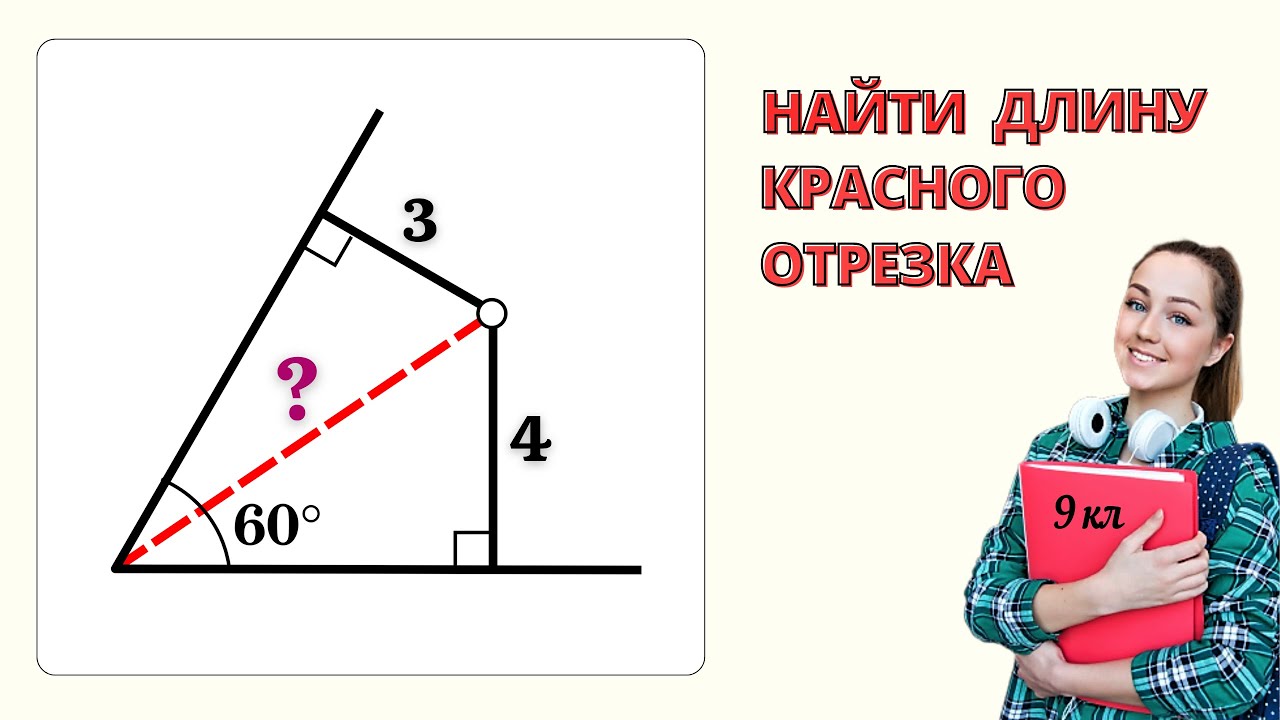
Дан угол A, равный 60 градусов, внутри него точка М, расстояния от которой до сторон угла равны 3 и 4. Найти расстояние от точки М до точки А.

[zawatsky]

Достроить общий треуг ещё вверх, получается известный 90/60/30. Видим, что тройка - его меньший катет, значит, гипотенуза того, что получился от тройки (общий верхний острый с большим треугом), будет 6, а общая высота таким образом - 10. Значит его основание 10/√3. Ну всё, осталось добить - зовём деда Пифагора: х²=4²+(10/√3)²=16+100/3=(48+100)/3=148/3=49¹/₃, отсюда

[ЭрнестоЧеГевара-пз]

Спасибо, за труд! Есть ещё решение.Рассматривая только два треугольника, обозначив один угол через j, а другой 60- j. Далее, sinj, sin(60-j). Найдем, tgj, из системы уравнений. У меня получилось около 6.

[constantinfedorov]

Четырехугольник вписанный, а красный отрезок - диаметр окружности. То есть, на безграмотно-геометрическом сленге, 2R. Это - раз. Расстояние между вершинами прямых углов - это хорда описанной окружности, на которую опирается вписанный угол 60°. То есть это сторона вписанного в эту окружность правильного треугольника, на том же сленге, R√3 (для суперпродвинутых - теорема синусов). Это - два. Но эта хорда - третья сторона вписанного треугольника, у которого две стороны 3 и 4, и угол между ними 120°. Это - три. Ну разумеется, никаких 5 не получится, там уже мелькает какой-то √37, а после некоторого усилия над собой - 2√111/3; (самое полезное знание в математике лично для меня, это 111/3 = 37)
На вопрос, 5 или не 5, легко ответить, ничего не считая. Диаметр окружности - самая большая его хорда, а расстояние между вершинами прямых углов (тоже хорда) заведомо больше 5 (5 было бы при прямом угле между 3 и 4)

[IvanQRT]

Моё решение такое:
1. Опускаем высоту из точки B: BH. На неё из точки M проводим перпендикуляр MK. Угол BMK 30°, соответственно отрезок BK будет половиной BM, 1.5. Остаток высоты KH будет равен MC, равен 4. Итого BH = 5.5 (11/2).
2. Треугольник ABH прямоугольный с углом 60°, из него AB = 2BH/√3 = 11/√3.
3. Треугольник ABM: AM = √(AB² + AM²) = √(121/3 + 9) = √(148/3) = 2√(37/3)

[МарияЯковлева-щя]

Можно решить, ничего не достраивая, и решение несложное.
Обозначим искомый отрезок за x. Найдём синусы двух углов, которые вместе составляют 60 градусов. Это 3/x и 4/x. Один из углов обозначим альфа, тогда второй равен 60 минус альфа.

Теперь используем формулы тригонометрии (синус разности и осн. триг. тождество) и составляем уравнение, в котором одна неизвестная величина x. Решаем уравнение и получаем ответ.

[arxippp-lbtv]

Угол 60 делится отрезком АМ на два угла, которые пропорциональны сторонам, на которые они опираются ввиду того, что вокруг АВМС описывается окружность. Или да?

[mikhailkadomtsev]

Ролик пока не смотрел, но напрашивается такое решение- продолжить перпендикуляр выше точки М. Получатся два прямоугольных треугольника с углами 30 градусов. Достроенный кусок перпендикуляра равен 6-и ( поскольку это гипотенуза маленького 30-и градусного), следовательно, катет большого треугольника: 6+4=10. Этот катет надо поделить на корень из трех, чтобы получить второй, меньший, катет большого 30-и градусного треугольника. Ну а далее- теорема Пифагора и находим длину искомого отрезка- корень квадратный из 148/3.

[vkr]

ВС стягивает дугу 120 градусов и в такой окружности можно по готовой формуле искать радиус описанной вокруг равностороннего треугольника стороной равной ВС окружности, R=BC*√3/3, !

[zawatsky]

Исходим из следующих соображений: 1. отрезок красный. 2. пунктирный. 3. рядом знак вопроса, розовый. Находим длину волны каждого цвета, вычисляем среднее арифметическое, не забываем и про нулевую интенсивность света в чёрных отрезках и белый шум белого фона. Да, учебник для девятого класса неспроста, потому ещё надо помножить на длину волос, поделить на треть суммы размеров бюста, бёдер и талии девочки и возвести в девятую степень. В итоге длина вычисляется через Е=mc² и приблизительно равна длине волоса из уха сферического коня в вакууме.☝👀

[adept]

Не мудрствуя лукаво: пар-мм на АМ как на диагонали. Его верхняя сторона =2√3.
АС = 2√3 + 4/√3.
Пиф уверен:
АМ = √(148/3).
Ваш 2-й способ дает такой же ответ, хотя это одно и то же.

[pojuellavid]

Коварство "точного" чертежа. Увидел ответ 7, но что-то меня удерживало от попытки доказательства АМ=ВМ+СМ.
Пересечем АВ и СМ в т. К. Из тр. ВКМ КМ=6 и СК=10. Из тр. АКС АС=10/√3. Из пифагоры АМС АМ^2=16+100/3
...и никаких девятых классов ...
Ответ:√(148/3)≈7, 02377

[Hyyudu]

Я провел из точки М отрезок, параллельный АС, до пересечения с АВ, получил точку К, потом опустил вниз перпендикуляр до АС, получил точку Т.
Треугольник ВМК с углами 30, 60, 90 и известным катетом 3 - находим ВМ. Треугольник АТК с углами 30, 60, 90 и известным катетом 4 - находим АМ. АМ+МВ = АВ, дальше у нас прямоугольный треугольник АВМ, по двум катетам по теореме Пифагора находим гипотенузу

[daniiltroshkov]

Можно через М провести прямую параллельно АС. Пусть точка пересечения К. Тогда угл ВКМ 60 градусов и напротив него сторона 3, значит ВК равен корень из 3х. Если из К опустить перпендикуляр на АС его длина будет 4. Напротив него угл 60 градусов, значит длина АК 8 поделить на корень из 3х. Значит длина АВ 11 поделить на корень из 3х. А дальше теорема Пифагора.

[lashman]

arcsin(3/x)+arcsin(4/x)=60 град --> -->
sin(sin^(-1)(3/x) + sin^(-1)(4/x)) = (sqrt(3))/2 --> x = 2 sqrt(37/3)

[TheAndyseitz]

Система
Сразу уходим от геометрии к алгебре.
╭
/ α+β=π/3
{ sin β = 4/x
\ sin α = 3/x
╰
tg α = 2√3/5
--> x=2√37/√3

Обычная строительная задача.

[sergeylopanov]

Решал достройкой вверх до треугольника. Сначала впал в ступор на секунду, получив ответ (√3*√148)/3, но потом дошло, √111)/3. Эх, мозги к 70-ти уже не те.🙂

[АмаЭльд]

Можно провести параллельную влево и перпендикуляр, от точки А к нему . Обозначим точку пересечения буквой Д, а точку пересечения с АВ, -буквой Е . Образуется два треугольника АДЕ и ВЕМ с углами 90°+60°+30° и прямоугольник . Найдя катет ДЕ и гипотенузу ЕМ найдём ДМ, затем найдём АМ . АМ²=ЕМ²×4², Но мне лень вычислять и особенно писать .

[sv]

Из точки С проводим СН перп-но АВ.
НВМС - трапеция, <MCH = <BAC = 60°
HC = BM + MC/2 = 3 + 4/2 = 5
AC = HC/sin60° = 10/√3
AM = √(AC² + MC²) = √(100/3 + 16) = (2/3)*√111
Ответ: АМ = (2/3)*√111

[КонстантинВинников-рб]

Так я и решил вторым способом, через тангенс 30°.

[КонстантинВинников-рб]

Решаемых задачу следующим образом: проводим сторону 3, для этого, продлеваем отрезок 3 и основание, до их пересечения, получим два прямоугольных треугольника, у которых, правый угол равен 30°, это значит, что продолжение отрезка 3 до пересечения с основанием, равно двум отрезками 4, то есть 8, а в сумме с отрезком 3 больший катет треугольника, равен 11, меньший катет, обозначим как a, относится к большему катера 11, как tg30°, то есть, a/11=1/√3, откуда a=11√3/3; теперь можно спокойненько найти x=3^2+(11√3/)^2=2√111/3, что примерно, равно 7, 02376916856...