Multivariable Calculus: Directional derivatives and the gradient

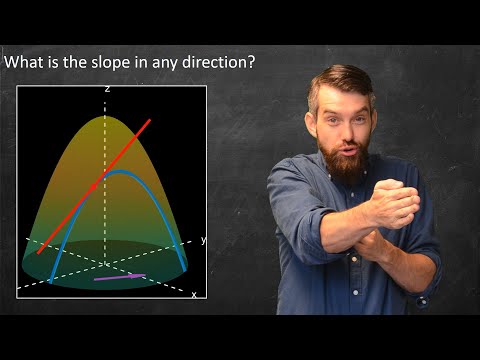
This lecture revisits directional derivatives in multivariable calculus. Directional derivatives extend the notion of partial derivatives by measuring the rate of change of a function in any direction, not just along the coordinate axes. Let's explore them further. (Multivariable Calculus Unit 3 Lecture 12)

Directional derivatives give us information about how a scalar-valued function changes as we move in a specific direction from a given point. Formally, if 𝑓:ℝ^𝑛→ℝ is a scalar-valued function, the directional derivative of 𝑓 at a point 𝐚 in the direction of a unit vector 𝐯 is defined as:

𝐷_𝐯𝑓(𝐚)=lim(ℎ→0) (𝑓(𝐚+ℎ𝐯)−𝑓(𝐚))/ℎ.

This definition generalizes the concept of partial derivatives. In fact, the partial derivatives with respect to the coordinate axes are just special cases of directional derivatives where 𝐯 is a standard basis vector.

A key result in multivariable calculus relates directional derivatives to the gradient of 𝑓. If 𝑓 is differentiable at 𝐚, the directional derivative in the direction of 𝐯 can be computed as:

𝐷_𝐯𝑓(𝐚)=∇𝑓(𝐚)⋅𝐯

Here, ∇𝑓(𝐚) is the gradient of 𝑓 at 𝐚, and the dot product captures the essence of how 𝑓 changes in the direction of 𝐯. The gradient vector points in the direction of the greatest rate of increase of 𝑓, and its magnitude gives the rate of increase in that direction.

The expression ‖∇𝑓‖⋅‖𝐯̂ ‖⋅cos(𝜃) offers significant insights into the behavior of multivariable functions, particularly in the context of directional derivatives. Here, ∇𝑓 represents the gradient of the function 𝑓, 𝐯̂ is a unit vector indicating the direction of interest, and 𝜃 is the angle between the gradient ∇𝑓 and 𝐯̂ . The key conclusions from this expression include:

1. Magnitude of the Gradient (‖∇𝑓‖):
- The magnitude of the gradient ‖∇𝑓‖ at a point gives the rate of the steepest ascent of the function at that point.

2. Direction of Maximum Increase:
- When 𝜃=0, cos(𝜃)=1, the directional derivative reaches its maximum value, indicating that walking parallel to ∇𝑓 results in the greatest increase in the function.

3. Direction of Maximum Decrease:
- When 𝜃=𝜋, cos(𝜃)=−1, the directional derivative is at its minimum, meaning walking in the direction opposite to ∇𝑓 leads to the greatest decrease.

4. No Change in Function Value:
- At 𝜃=𝜋2, cos(𝜃)=0, indicating no change in the function value when moving perpendicularly to ∇𝑓.

5. Unit Vector (‖𝐯̂ ‖):
- The magnitude of 𝐯̂ is always 1, simplifying the expression to ‖∇𝑓‖⋅cos(𝜃).

6. Cosine of the Angle (cos(𝜃)):
- The factor cos(𝜃) determines the component of the gradient's magnitude contributing to the directional derivative in the direction of 𝐯̂ .

The geometric interpretation of directional derivatives and gradients is foundational in understanding the behavior of multivariable functions. For example, the gradient being orthogonal to level curves provides insights into how a function changes near critical points. The ability to determine the direction of steepest ascent or descent is crucial in fields like optimization and physics.

#mathematics #multivariablecalculus #directionalderivatives #partialderivatives #gradient #iitjammathematics #calculus3

[armaansengupta]

Towards the very end of that video, the path shown is the steepest, so does that mean it would also have the shortest distance to get from the bottom valley to the top peak?