filmov
tv
🟡09a - Directional Derivatives and the Gradient Vector 1

Показать описание
In this lesson, we are going to discuss Directional derivatives and the gradient vector.
Ever since, we've been looking at the partial derivatives fx and fy which represent the rate of change of the function directed along the x and y axis respectively.
In this lesson we want to determine the rate of change of a function as both x and y are varied simultaneously.
The directional derivative of a functions at a point x,y in the direction of an arbitrary unit vector is given by:
Duf(x,y) = fx(x,y)a + fy(x,y)b
We shall focus more on directional derivatives and introduce the gradient vector in the next lesson
00:00 - Introduction
04:34 - Ex 1
12:09 - Ex 2
19:41 - Ex 3
Playlists on various Course
1. Applied Electricity
2. Linear Algebra / Math 151
3. Basic Mechanics
4. Calculus with Analysis / Calculus 1 / Math 152
5. Differential Equations / Math 251
6. Electric Circuit Theory / Circuit Design
7. Calculus with Several Variables
Make sure to watch till the end.
Like, share, and subscribe.
Thank you.
Ever since, we've been looking at the partial derivatives fx and fy which represent the rate of change of the function directed along the x and y axis respectively.
In this lesson we want to determine the rate of change of a function as both x and y are varied simultaneously.
The directional derivative of a functions at a point x,y in the direction of an arbitrary unit vector is given by:
Duf(x,y) = fx(x,y)a + fy(x,y)b
We shall focus more on directional derivatives and introduce the gradient vector in the next lesson
00:00 - Introduction
04:34 - Ex 1
12:09 - Ex 2
19:41 - Ex 3
Playlists on various Course
1. Applied Electricity
2. Linear Algebra / Math 151
3. Basic Mechanics
4. Calculus with Analysis / Calculus 1 / Math 152
5. Differential Equations / Math 251
6. Electric Circuit Theory / Circuit Design
7. Calculus with Several Variables
Make sure to watch till the end.
Like, share, and subscribe.
Thank you.
🟡09a - Directional Derivatives and the Gradient Vector 1
Directional Derivatives and Gradient Vectors - Part 1 [Dr. Scott Adamson]
Directional Derivatives and the Gradient
🟡09c - Maximum Rate of Change (Directional Derivatives and the Gradient Vecctor 3)
Directional Derivative Examples
🟡09b - Find The Gradient Vector and Directional Derivative of the Function 2
Directional Derivative Justification Using the Chain Rule
Concept about Directional Derivative
Gradient and Maximum Directional Derivatives
Calculus 3 - Directional Derivative & Gradient Properties
Calculus BC Unit 7, Lesson 9a: Vector-Valued Functions
Velocity & Acceleration - Calculus III (full course) - lecture 09a (of 24)
Vector calculus lecture 9a
LCS - 09a - Mechanical systems with rotational and translational displacement
MH1811 Tutorial 3 question 1
Tensor Calculus Lecture 10c: The Second Order Normal Derivative
Tensor Calculus Lecture 9a: The Equations of Surface and the Shift Tensor
Calculus III Final Exam Review 5: Line Integrals and Green's theorem
Calculus 1.2d - Derivative from a Graph
Physics 9A - Lecture 11
Drillstring and Drilling Dynamics: Part 9a - Sinusoidal Buckling
The Differential Equation for Fluid Acceleration
calculate (a) E1 and D1, (b) P2 and Ppv2 , (c) the energy density for each region.- E-Field
🟡07b - Chain Rule for Partial Derivatives 2 of (Multivariable Functions)
Комментарии
 0:25:46
0:25:46
 0:17:48
0:17:48
 0:13:20
0:13:20
 0:21:50
0:21:50
 0:06:32
0:06:32
 0:23:11
0:23:11
 0:06:25
0:06:25
 0:06:47
0:06:47
 0:03:06
0:03:06
 0:31:10
0:31:10
 0:15:11
0:15:11
 0:54:18
0:54:18
 0:23:38
0:23:38
 0:15:21
0:15:21
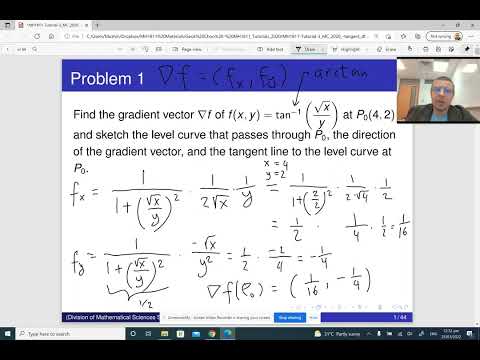 0:10:58
0:10:58
 0:17:04
0:17:04
 0:59:42
0:59:42
 1:03:28
1:03:28
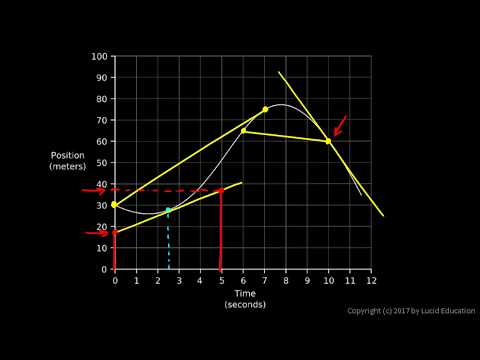 0:09:39
0:09:39
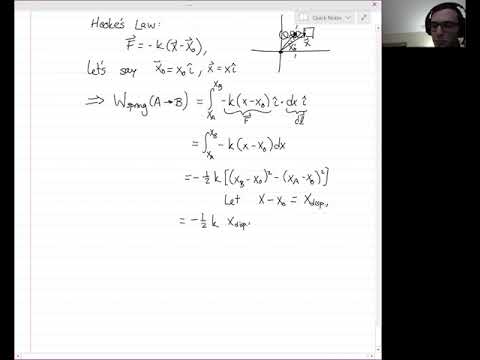 0:47:29
0:47:29
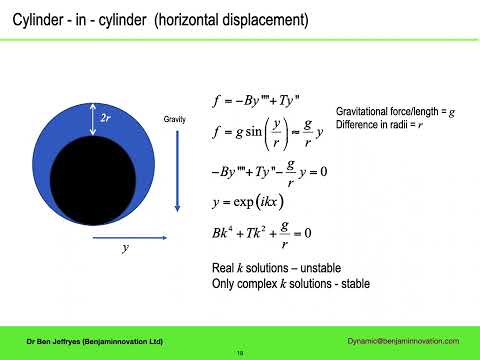 0:23:02
0:23:02
 0:27:42
0:27:42
 0:18:30
0:18:30
 0:13:44
0:13:44