How to solve the three-circle problem from the 2022 GCSE math exam

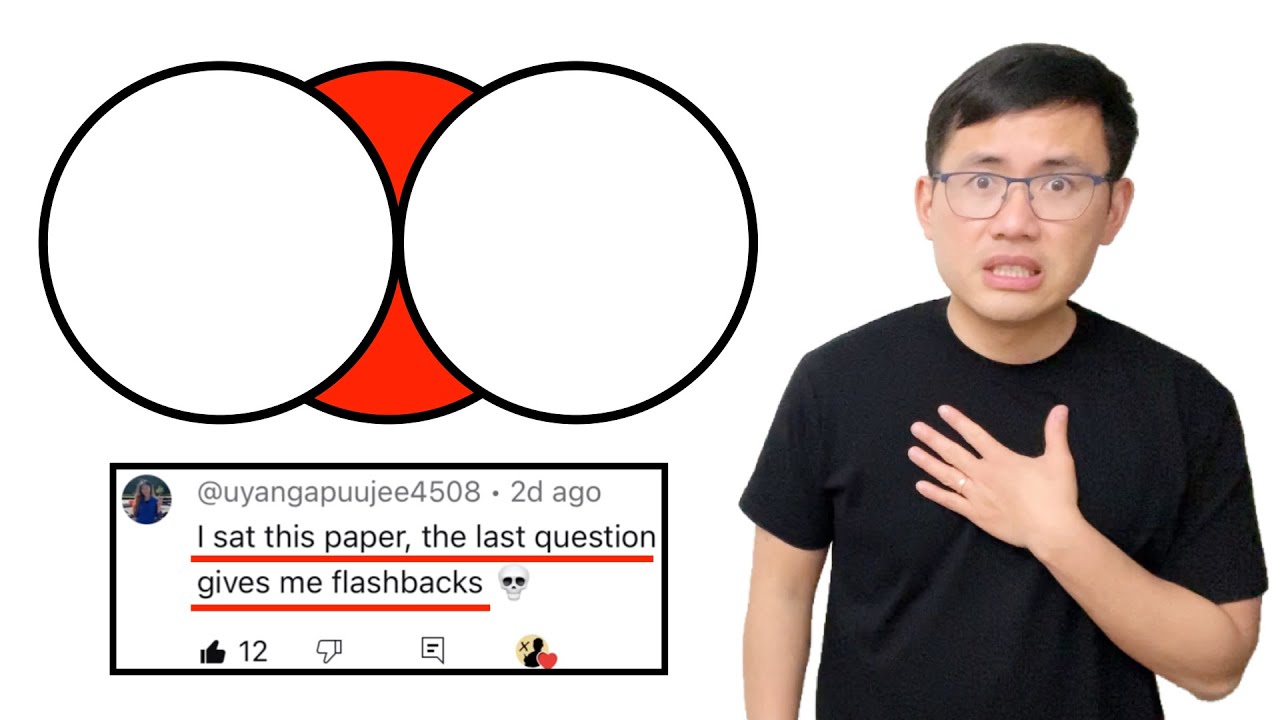
Here's the last question from the 2022 GCSE maths paper that made the news. We have three circles as shown and each radius is 4 cm. We have to find the area of the shaded region in the middle. I made a horrible mistake last time when I said the area of a circular sector is r*theta. The correct formula should be A=1/2*r^2*theta and theta has to be in radians.

----------------------------------------
Big thanks to my Patrons for the full-marathon support!
Ben D, Grant S, Erik S. Mark M, Phillippe S.

[thesounddisciple]

Bruh so many people here saying how clever they are and that they have no idea how this is "notorious". Its a GCSE question done by all 16 yo a lot of whom have no interest in maths, just because youre doing complex analasis or linear algebra at college or uni doesnt mean that a 16 yo kid cant struggle without you saying how much better you are, why cant we appreciate that some people struggled and be happy that this vid might help

[aerospace]

Great video. The only comment I will make as someone who teaches maths here in the UK, is radians are not taught until A level (beyond GCSE). GCSE students are taught area of a sector by considering it a fraction of the area of the whole circle using degrees: (theta/360) multiplied by pi.radius^2

[Calculus]

You wouldn’t be expected to know about radians at GCSE. The area of the sector is one sixth of the area of a circle.

[sampan]

This was in the non-calculator exam and it brought back some funny memories of the exam, it's nice you're covering it nice video!

[tanelkagan]

The "rule of thumb" I give my students is spend on average 1 minute per mark. This is based on a 90 minute exam, for 80 marks, with 10 minutes for checking work.

Of course there are some 1 mark questions at the start of the paper that can be answered in seconds, and I think you really do need to work quickly on those basic questions to build up a time cushion because in my view some of these later questions can be quite involved, and will take longer (in minutes) than the number of marks being awarded.

This was a video of over 8 minutes and yes, there was some time taken for explanation etc but as a calculus professor BPRP knows exactly where to start and which direction to take. I think most 15-16 year olds would in any event take longer than 5 minutes to answer it, especially given the number of steps and the need to methodically set out working.

I do think that's a bit of a shame as it over-rewards simple questions and under-rewards the difficult ones. If I were designing the paper I would increase the number of marks and keep the very basic questions that can be answered in 30 seconds or less at 1 mark, whilst weighting the difficult questions (normally up to 5/6 marks) more and giving them say 10 marks.

Exam boards should be able to work out what is the required amount of time to spend on a question, and allocate marks accordingly, but until they do that, I'll keep advising (a) pick up the easy marks quickly (b) don't dwell on a question too long, move on to the next and (c) come back later if you have time". That's general exam strategy, not specific to maths, of course.

[AndrewJohnson-urlw]

GCSE maths will only be in degrees no angles in radians. Radians are only introduced to maths students doing A level in the UK.

[crtwrght]

An alternative approach is to find a segment of either of the outer circles (radius 4cm, angle of 120 degrees (since radians aren't technically in the GCSE syllabus)) and then multiply that by 4 and subtract from 16pi.

[tomlopez]

I looked at this paper as a final year engineering student and it stumped me for a few minutes too

[Lil_electrician]

For the people in the comments ! Yes this question isn’t incredibly hard to solve if you know your stuff, but remember that most of the students that did this question were 16 year olds that dgaf with probably around 5~10 minutes left if lucky 😭

[bharadwajkk]

I just did integration, I converted it into geometric coordinates considering B as origin, found each coordinate, found equations of the circles, found points of intersection of the circles the integrate from 0 to 2 for 1 part, , then 16pi-8(segment area) = ans, should mention each segment is that area from 0-->2 that's part of the A and C circles that are 8 in total

[akaRicoSanchez]

I did it slightly differently with a mix of geometry and basic algebra: if you draw some additional circles of radius 4 centered on intersections, you can partition the central circles into 6... let's call them concave triangles (CT) and 12 ... almonds (A). The grey area is then equal to 2CT + 2A. Since the circles have radius 4, we know 6CT + 12A = 16Pi and we also know that the area of an equilateral triangle of side 4 can be described as follow CT + 3A/2 = 4 Sqrt(3). From there you manipulate these two equations to reach 2CT + 2A = 16 Sqrt(3) - 16 Pi / 3.

[calbernandhowbe]

I was feeling so confident going into this exam, i finished the rest of the paper with half an hour left and i thought it was going so well, and then the last question hit me 😭it took me all of that remaining half hour to solve this!!

[upasiensis]

A less cumbersome method:

Call the upper intersection of the circles A and B, Y, and that of B and C, X.

BX=BC=XC=4. BCX is therefore equilateral, so 6 such triangles will form a hexagon in Circle C. Call each triangle area A(T)
Equally, Circle C comprises 6 pie slices of equal size - the triangles plus a curved portion. Call each slice area A(P). It's just 1/6 of the area of the circle.

Next, the part in each slice but not in each triangle is a sliver. Call the sliver area A(S)

But also BXY is another congruent triangle, and half the area we want, with 2 slivers extra.

So for the whole of the desired area, we need 2A(P)- 4(A(P)-A(T)) = 4A(T)-2A(P)

A(P) = 1/6(pi*4^2)
A(T) = 1/2(4*(2sqrt(3))
4A(T)-2A(P) = 2(4*(2sqrt(3))-1/3(pi*4^2) = 16sqrt(3)-16pi/3

[YousefToday]

I got

|(-16π - 48 √3) ÷ 3|
without using the formula.

I divided B into 6 equal pieces, then made a triangle for every piece.

I calculated the area of the triangle (At).
Then I calculated the area of the small thing left,
As = (⅙ circle B - At).

Finally, it will be

Shaded Area = 16π - ((As ×8) + At×4).

I simplified and got my answer.

[tomctutor]

Since 1 circle is made up of 6 equilateral triangles and 6 minor segments:
Let O = area of a circle = πr²
let ∇ = area of equilateral triangle = ¼r²√3
let ⌓ = area of minor segment =?
let ⋎ = shape internal to area of ∇ such that, ∇= ⋎ +2⌓
hence we can form a system of simultaneous equations;

A = area required = 2⋎ + 2⌓
O = 6∇ + 6⌓
∇ = ⋎ +2⌓

Solving for unknown ⌓ by seeing that
2⌓ = ⅓O -2∇
2⋎ = 6∇ - ⅔O

adding these two eqn. gives solution,
A = (⅓O -2∇) + (6∇ - ⅔O)
= 4∇ - ⅓O
= 4(¼r²√3) -⅓(πr²)

sub in r= 4cm
gives area A = 16(√3 - ⅓π) cm² ㋡㋡

[yurfwendforju]

The worst thing is my math teacher put a somewhat similar question for me on the board, just because I do calculus in my free time, and judging by his face, he wanted me to find it's area without a limit. Solved it like you did. After class he told me, that he wanted it to be somehow get solved with the golden ration, like wtf. anyway, got an A :)

[thirstyCactus]

Here is a different way to do it: Let AB = 1, then let D be the upper point of intersection between circles A and B. Then find angle, E, between segments AB and BD. Drop vertically down from D, point F, at intersection of segment AB. Point F must be mid-point of AB. Thus, from right-triangle, Z, formed by FB, BD, DF, angle E can be solved by arccos(BF / BD) = arccos(1/2) = pi/3. Area of corresponding sector is then, Y = pi/3 * 1/2 * r^2. Radius is same as segment AB, so sector area becomes, Y = pi / 6. Area of triangle Z is 1/2 * BF * DF. Because Z is equilateral, it height, segment DF, is srq(3)/2. Area of Z is then 1/2 * 1/2 * sqr(3)/2 = sqr(3)/8. The area of one full circle, W, is pi*r^2. Because r = 1, W = pi. Then, to get the area in question, V, that's the circle, W's, area minus 8 slivers; each sliver is sector, Y, minus triangle, Z. Or, W = V - 8 * (Y - Z) = pi - 8 * ( pi/6 - sqr(3)/8 ) = pi - (8/6)*pi + sqr(3) = sqr(3) - (2/6)pi. To get the final answer, V, requires scaling AB back up to 4, which results in 16 times the original calculated area, or 16 * V = 16*sqr(3) - (16/3)*pi. I actually paused the video this time! :D It's basically the same way blackPenRedPen solved it, but using the full circle, instead of a quarter-circle.

[rdinary_guy]

For the area of equilateral triangle, wouldn't it be easier if we just use "Area = 1/2 ab sin C"?

[MathProdigy]

I believe the first time you tried solving this problem, you used the formula r multiplied by theta, which is used to find the arc length of a certain section of the circle.

[jeremielhomme]

You could have gone the calculus way by integrating (r^2 - x^2)^{1/2} - r/2 from x = - r*sqrt(3)/2 and + r*sqrt(3)/2. After that you just need to substract 4 times the result to the area of the circle. Not sure if it is faster, though.