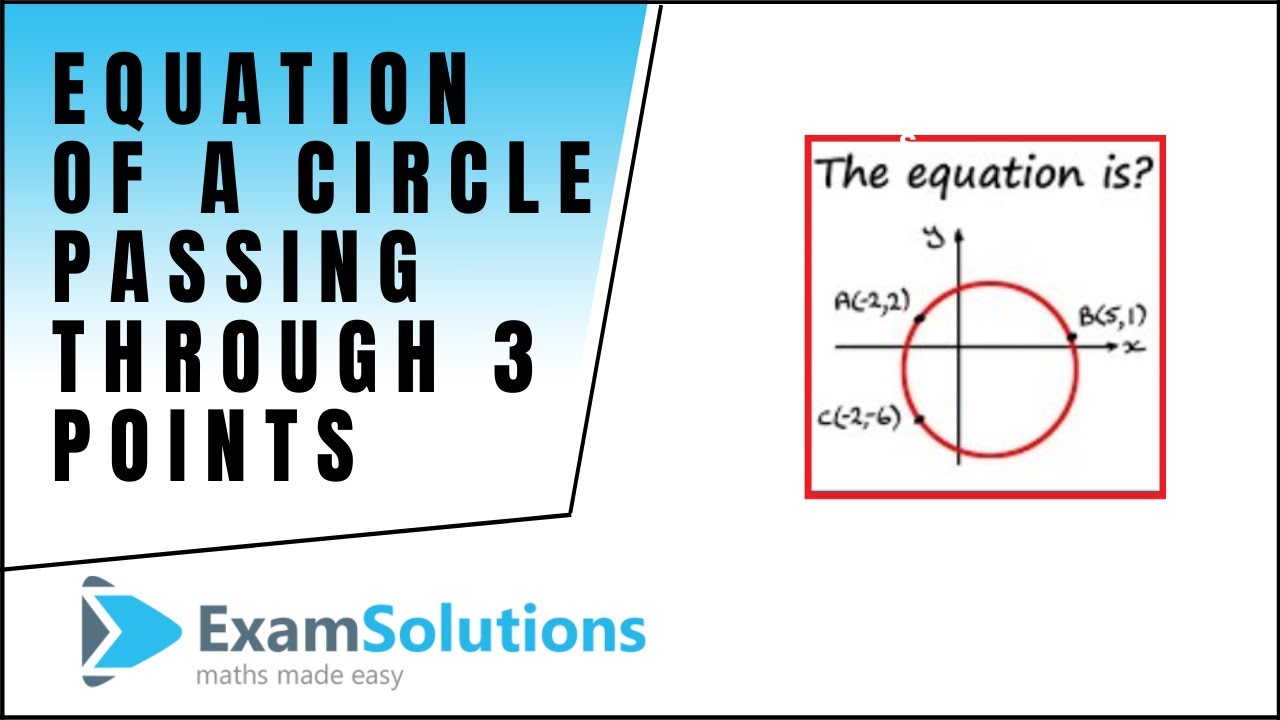
Equation of a Circle passing through 3 points | ExamSolutions

Equation of a circle.

Here I show you how to find the equation of a circle passing through 3 points on the circumference.

NEW COLLAB 2022!! Proudly partnered with @PrimroseKitten to create BETTER resources.

[michellesilva]

Why do I love exam solutions? Simply it’s amazing especially when you’re stuck in a question and have no one to

[joshuamallon]

you sound happy as mate u really make revising fun . u the man appreciate ya !

[cfgauss]

Outstanding explanation! The intersection of the chords' perpendicular bisectors is the key!

[nirmitchanana]

Could you please go through the edexcel a level 2019 mock exams please

[ameliamos]

i think ill actually get this question right on exams now thank you

[shararzaid]

Alright I'm feeling charitable so if any of you noobs are finding this hard then may I suggest a more formulaic approach?

1) Consider the general equation for a circle : *(x−x₁)²* *+* *(y−y₁)²* *=* *r²*

Plug in the three points to create three quadratic equations.

2) Now there should be 3 equations like:

*(x−a)²* *+* *(y−b)²* *=* *r²* *①*
*(x−c)²* *+* *(y−d)²* *=* *r²* *②*
*(x−e)²* *+* *(y−f)²* *=* *r²* *③*

3) Subtract the *①* from the *②* which will create another equation that's linear, call it ④ and subtract ① from ③, call it ⑤

4) Solve the two Simultaneous linear equations:

*ax* *+* *by* *=* *c* *④*
*dx* *+* *ey* *=* *f* *⑤*

which will give you the center coordinate points of the circle.

5) Last step is to plug the center points into any of the ①, ② or ③ equations and solve for *r* and the rest is history.

[kakashi]

You videos are very helpful sir. I hope you continue to upload more content. From India!

[andydaniels]

The point-normal form of equation of a line (i.e., n·x = n·p) seems more convenient and less error-prone in this application. For instance, to find the equation of the perpendicular bisector of AB, we compute n = B-A = (7, -1) and the midpoint p = (A+B)/2 = (3/2, 3/2), yielding (7, -1)·(x, y)=(7, -1)·(3/2, 3/2) or 7x-y=9.

[bhagyaamarasinghe]

Thank you so much. This helped me a lot. :)

[file]

ahhh such an amazing video thank you!!

[hesterclapp]

Is there a way to calculate a circle from point A, point B and a tangent passing through point A?

[itsshreyshrey]

Thank you for making maths videos for us! You have helped me raise my grades a lot! ❤️

[AfricanTalesByMum]

you are the best you have made me understand this concept

[ahnafjawad]

thanks been dying over a sum like this

[johnlynch]

Is this still relevant to the AQA spec? I’ve not come across it at all

[syp]

2:57 how did you know that was the center?

[brandongudoy]

What if it doesnt have vertical or horizontal line? What formula is needed?

[omaribrahim]

Can you please do worked solutions for M1 IAL past papers? Please, I really need your help. All of your C12 solutions were super useful

[ahmetlushi]

How many marks would these sort of questions be worth in a typical exam ?

[princesstrayvilla]

Hey! Can I ask about the gradients? If the gradient is positive, does it become negative as a perpendicular gradient?