filmov
tv
Can You Find the Area of the BIG Circle? | Quick and Easy Tutorial
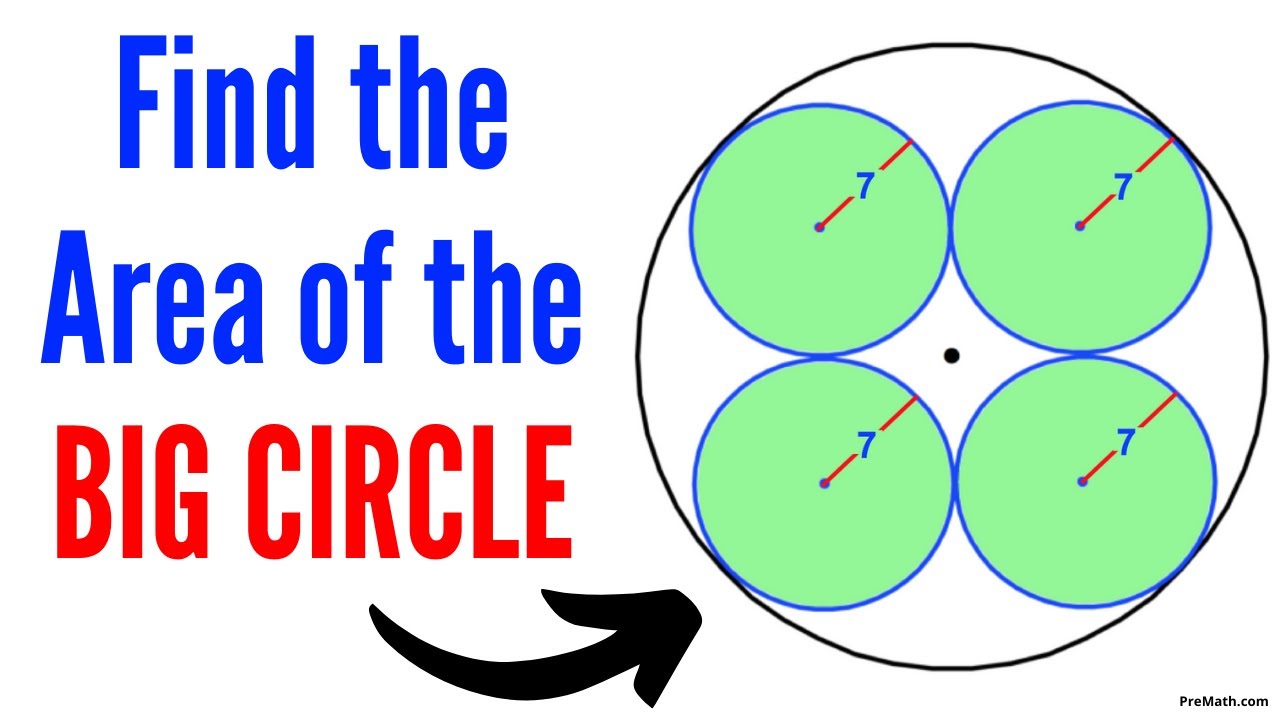
Показать описание
Find the Area Challenge
Math Antics - Area
Can you find area of the Purple shaded region? | (Rectangle) | #math #maths | #geometry
Area for Kids
Can YOU find the area? – Math problem
Finding the Area of a Composite Figure | Area of Composite Rectangles
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
Can you find the area of the Pentagon??
Can you find area of the Blue triangle? | (Fun Geometry Problem) | #math #maths | #geometry
How to Find the Area of a Rectangle | Math with Mr. J
How to Find the Area of a Square | Math with Mr. J
Can you find the Area of the Green Shaded Region? | Double Semicircles
Find the Area of an Equilateral Triangle
Can you find area of the Green shaded triangle? | (QuarterCircle) | #math #maths | #geometry
Can you find area of the Rectangle? | (Justify your answer) | #math #maths | #geometry
Find Perimeter, Area & Diagonal of Square | #shorts #shortvideo #viral #trending #mathsshorts
Can You Find The Area?
Area of square | How to find area of the square #shorts
Can you find area of the Pink shaded Quadrilateral? | (Right Triangles) | #math #maths | #geometry
Can you find the Area of the Green Shaded Region? | 2 Simple Methods
Geometry Puzzle | Can You Find The Area?
Can you find area of the Purple shaded Trapezoid? | (Right Triangles) | #math #maths | #geometry
Area of rectangle | How to find area of a rectangle #shorts
can you find the Area? #area #maths #circle #brain brai #olympiad #exam #mathematics #mathway
Комментарии
 0:04:33
0:04:33
 0:10:26
0:10:26
 0:09:12
0:09:12
 0:08:58
0:08:58
 0:05:18
0:05:18
 0:07:14
0:07:14
 0:22:10
0:22:10
 0:01:52
0:01:52
 0:13:19
0:13:19
 0:04:43
0:04:43
 0:02:48
0:02:48
 0:08:28
0:08:28
 0:00:47
0:00:47
 0:09:56
0:09:56
 0:10:00
0:10:00
 0:00:13
0:00:13
 0:04:29
0:04:29
 0:00:30
0:00:30
 0:12:14
0:12:14
 0:10:49
0:10:49
 0:01:39
0:01:39
 0:12:38
0:12:38
 0:00:30
0:00:30
 0:00:41
0:00:41