filmov
tv
3.2 - Local & Absolute MAX & MIN Points (full lesson) | grade 12 mcv4u | jensenmath.ca

Показать описание
In this lesson you will learn how to use the first derivative test to find local max/min points of a polynomial function. A local max exists at a point if at the point, the derivative is zero, before the point the derivative is positive (function increasing), and after the point the derivative is negative (function is decreasing). A local min exists at a point if at the point, the derivative is zero, before the point the derivative is negative (function decreasing), and after the point the derivative is positive (function is increasing). When finding an absolute max or min, test endpoints of interval and critical numbers.
Absolute Maximum and Minimum Values of Multivariable Functions - Calculus 3
3.2 - Local & Absolute MAX & MIN Points (full lesson) | grade 12 mcv4u | jensenmath.ca
Calc I: Graphing a function given local and absolute max/min
Finding Absolute Maximum and Minimum Values - Absolute Extrema
📈 Local and Absolute Maximum and Minimum from a Graph 📈
Absolute Maximum and Minimum Values - Finding absolute MAX & MIN of Functions - Calculus
Absolute Maximum and Minimum Values of Multivariable Functions (Part 1)
Find the absolute maximum and minimum value of f on [-2,3]. F(x) = 2x^3 - 3x^2- 12x +1
Section 3.2.2 - Local and Absolute Extrema Ex.3
Learn how to find the absolute max, min and relative max min of a graph
Video3166 - Calculus 3 - Absolute Maximum/Minimum - Bounded Region - Part 1/2
Finding the Absolute Extrema on a Closed Interval Example with f(x) = x^3 - 12x
Absolute max and min values Problem 1 (Multivariable Calculus)
Calculus: Absolute Maximum Minimum for Polynomial First Derivative Application
WHAT IS LOCAL MAXIMA AND LOCAL MINIMA ABSOLUTE MAXIMA AND ABSOLUTE MINIMA
Differential Calculus | Find absolute maximum & minimum value of f(x)=3x^4–4x^3–12x^2+1 in [-2, ...
Derivatives 7 (Application of Derivatives III - Absolute Maximum/Minimum & Local Maximum/Minimum...
Absolute and Local Extrema
Read Absolute and Local Maximum Minimum Value from Graph
Calc III: Find absolute max/min on a Domain
🟡14a - Absolute Minimum and Maximum of Multivariable Functions 1
Absolute Maximum and Minimum of f(x) = sin(x) + cos(x) over an Interval
Absolute Maximum and Minimum Values of Multivariable Functions (Part 2 of 2)
Absolute Maximum & Minimum
Комментарии
 0:11:24
0:11:24
 0:24:49
0:24:49
 0:02:11
0:02:11
 0:17:17
0:17:17
 0:03:27
0:03:27
 0:09:15
0:09:15
 0:06:18
0:06:18
 0:04:57
0:04:57
 0:04:57
0:04:57
 0:02:41
0:02:41
 0:11:10
0:11:10
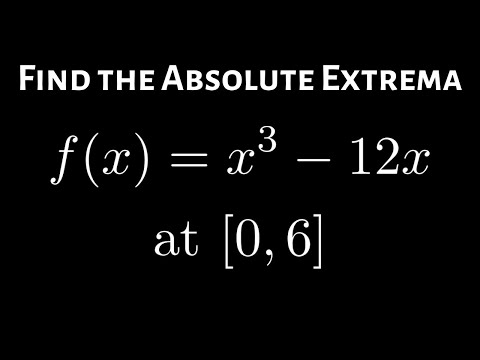 0:03:23
0:03:23
 0:25:26
0:25:26
 0:05:21
0:05:21
 0:02:21
0:02:21
 0:12:34
0:12:34
 0:23:26
0:23:26
 0:09:45
0:09:45
 0:06:26
0:06:26
 0:07:42
0:07:42
 0:20:02
0:20:02
 0:05:43
0:05:43
 0:11:19
0:11:19
 0:01:00
0:01:00