filmov
tv
Session 8: Inner products, vector norms, dual spaces, introduction to matrix norms

Показать описание
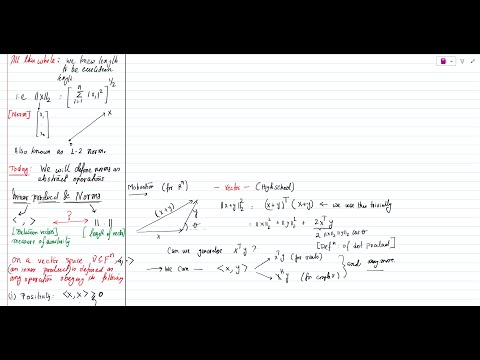
This closes the discussion on linear algebra. To begin with, it introduces the concept of distance and similarity in a vector space and uses it to motivate inner products and norms. It links inner products and norms too. It states its axioms and uses them to prove the Cauchy-Schwartz inequality.
Once, norms were introduced, dual spaces were discussed followed by the maths behind dual norms. It shows the geometry of the dual of the L1 and L2 norms. Eventually, it describes Lp norms and their dual (1/p + 1/q = 1, p, q \geq 1).
After discussing the vector norms, we defined matrix norms on Mn and induced matrix norms and discussed their relevant properties. Some of them are - the Frobenius norm and the L1-induced matrix norm.
Once, norms were introduced, dual spaces were discussed followed by the maths behind dual norms. It shows the geometry of the dual of the L1 and L2 norms. Eventually, it describes Lp norms and their dual (1/p + 1/q = 1, p, q \geq 1).
After discussing the vector norms, we defined matrix norms on Mn and induced matrix norms and discussed their relevant properties. Some of them are - the Frobenius norm and the L1-induced matrix norm.
 2:43:07
2:43:07
 0:23:02
0:23:02
 0:34:12
0:34:12
 0:02:11
0:02:11
 0:11:18
0:11:18
 0:23:09
0:23:09
 0:08:06
0:08:06
 0:31:57
0:31:57
 0:06:20
0:06:20
 0:55:10
0:55:10
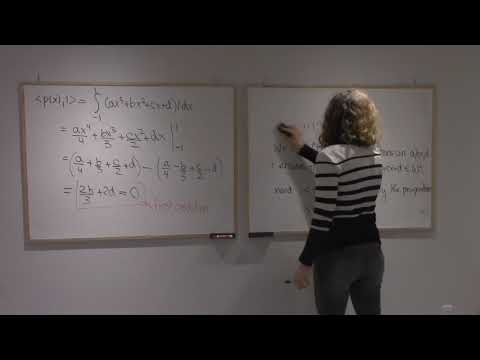 0:06:08
0:06:08
 0:19:05
0:19:05
 1:04:19
1:04:19
 0:12:24
0:12:24
 0:20:17
0:20:17
 0:05:44
0:05:44
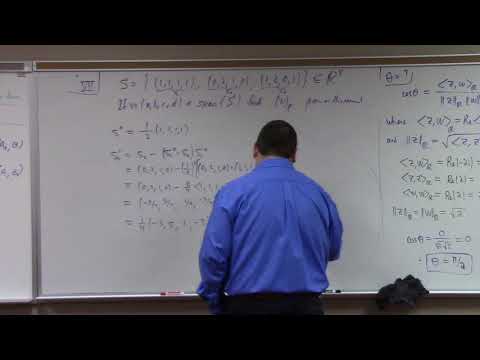 0:10:13
0:10:13
 0:59:51
0:59:51
 0:11:48
0:11:48
 0:39:59
0:39:59
 1:12:24
1:12:24
 0:34:06
0:34:06
 0:27:40
0:27:40
 0:30:33
0:30:33