filmov
tv
Montrer qu'une Fonction a PLUSIEURS VAR est C1 - Explications & Exemple - Maths Bac+1 / Bac+2

Показать описание
A travers un exemple, on va voir le raisonnement pour montrer qu’une fonction à plusieurs variable est C1. Cela nous permettra de revoir les notions de continuité (par changement de variables et méthode des suites) et dérivabilité.
Dans cette vidéo :
0:00 Intro & présentation
0:51 Continuité
2:15 Dérivabilité
4:28 Création de nouvelles fonctions
6:07 Continuité des dérivées
9:55 Fin
Précision : dans cette vidéo, on ne rédigera pas tout de manière absolument parfaite, afin de gagner du temps, on fera quelques raccourcis (mais qui seront bien évidemment précisés).
On répondra aux questions :
- Comment montrer qu’une fonction est C1 ?
- Comment étudier la continuité des dérivées partielles ?
- Que signifie C1 pour les fonctions à plusieurs variables ?
- Comment montrer qu’une fonction n’est pas C1 ?
- Comment montrer que les dérivées partielles sont continues ?
- Comment montrer que les dérivées partielles ne sont pas continues ?
J'essaye de bien expliquer :) ... en 4K 😝
Fonctions à plusieurs variables - Analyse Maths - Maths - Prépa/Licence/IUT/BTS 1e ou 2e année
Dans cette vidéo :
0:00 Intro & présentation
0:51 Continuité
2:15 Dérivabilité
4:28 Création de nouvelles fonctions
6:07 Continuité des dérivées
9:55 Fin
Précision : dans cette vidéo, on ne rédigera pas tout de manière absolument parfaite, afin de gagner du temps, on fera quelques raccourcis (mais qui seront bien évidemment précisés).
On répondra aux questions :
- Comment montrer qu’une fonction est C1 ?
- Comment étudier la continuité des dérivées partielles ?
- Que signifie C1 pour les fonctions à plusieurs variables ?
- Comment montrer qu’une fonction n’est pas C1 ?
- Comment montrer que les dérivées partielles sont continues ?
- Comment montrer que les dérivées partielles ne sont pas continues ?
J'essaye de bien expliquer :) ... en 4K 😝
Fonctions à plusieurs variables - Analyse Maths - Maths - Prépa/Licence/IUT/BTS 1e ou 2e année
Montrer qu'une Fonction a PLUSIEURS VAR est C1 - Explications & Exemple - Maths Bac+1 / Bac...
Montrer qu'une fonction EST / N'est PAS DIFFÉRENTIABLE sur un INTERVALLE - Méthode & E...
Montrer qu’une fonction de plusieurs variables est continue - mathématiques 1
Montrer qu'1 FONCTION à PLUSIEURS VAR a une LIMITE hors de L'ORIGINE/est CONTINUE -Méthode...
Montrer qu'une fonction EST / N'est PAS DIFFÉRENTIABLE en un POINT - Méthode & Exemple...
Fonctions à deux variables:Montrer qu’une fonction est différentiable et de classe C^1
LE COURS : Continuité d'une fonction - Terminale
Montrer qu'une FONCTION à PLUSIEURS VARIABLES a une LIMITE en L'ORIGINE - Méthode & Ex...
LIVE Astrotarotina - Pierre Treuil
Montrer qu'1 FONCTION à PLUSIEURS VARIABLES N'a PAS de LIMITE en un POINT -Méthode & E...
Fonctions : limites, continuité. Cours MPSI, PCSI, PTSI, prépa HEC, BCPST
Montrer qu'une fonction est décroissante sans dériver 😵💫
Montrer que la fonction f admet un maximum
Montrer qu'une FONCTION est CONTINUE - Exercice Corrigé - Terminale
Comment montrer qu'une fonction est continue ?
exo 1061 : montrer qu'une fonction de deux variable n'est pas de classe C1
Montrer qu'une fonction est prolongeable par continuité
Montrer Qu'une Fonction Est Affine Par Intervalles Acte 1
Montrer que toutes les courbes de fonction fn(x)=(x²-2x)^n passent par 4 points fixes - type bac
Méthode 1: montrer qu'une fonction est une fonction de répartition
Montrer qu'une fonction n'est pas croissante
Comment automatiser un fichier #excel avec la fonction SI #si #tips #calcul
2 fonctions cachées de l'Apple Watch
Astuce pour apprendre les valeurs de trigo 👌
Комментарии
 0:10:19
0:10:19
 0:03:29
0:03:29
 0:08:09
0:08:09
 0:05:11
0:05:11
 0:12:49
0:12:49
 0:18:31
0:18:31
 0:24:17
0:24:17
 0:07:03
0:07:03
 2:19:02
2:19:02
 0:06:02
0:06:02
 0:28:01
0:28:01
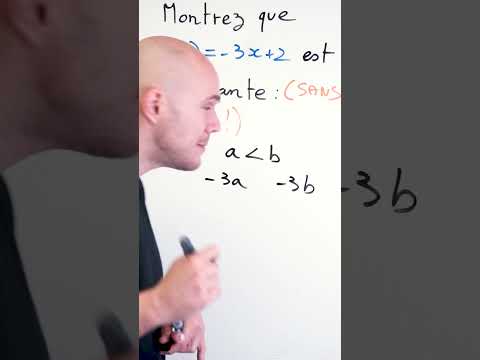 0:01:00
0:01:00
 0:07:31
0:07:31
 0:05:14
0:05:14
 0:05:19
0:05:19
 0:05:27
0:05:27
 0:07:56
0:07:56
 0:12:52
0:12:52
 0:07:39
0:07:39
 0:23:40
0:23:40
 0:04:32
0:04:32
 0:00:31
0:00:31
 0:00:23
0:00:23
 0:01:00
0:01:00