filmov
tv
Prove it! Properties of logarithms

Показать описание
In this video, I prove the properties of logarithms like ln(xy) = ln(x) + ln(y) by using the integral definition of the logarithm. Enjoy!
06 - Proving the Logarithm (Log) Rules - Understand Logarithm Rules & Laws of Logs
Prove it! Properties of logarithms
Proving the laws of logarithms
Prove a Property of Logarithms
Defining the natural logarithm
Proving Logarithmic Equations - College Algebra & Precalculus
Change of base formula proof | Logarithms | Algebra II | Khan Academy
Prove Logarithmic Identities. Properties of Logarithms. P8
Proofs of properties of logarithms
Prove: Addition and Subtraction Properties of Logarithms
Solving Log Equation
Natural Logarithms
Can You Prove This Property of Logarithms?
proving ALL logarithm properties using calculus
LAWS OF LOGARITHM with solved examples.
Cat Derive Inverse Properties of Logarithms #maths #proof #derive #science
Logarithmic Form to Exponential Form (Natural Log Edition) 🤯 #Shorts #algebra #math #education
The Untaught Logarithm Property
properties of logarithm with proof
How to Prove the Power Rule for Logarithms
Cat Derive Power Rules Properties of Logarithms V2 #maths #proof #derive #science
Properties of Logarithms - Proof of Property 1
Proving the Change of Base Formula for Logarithms #shorts
Logarithms, Explained - Steve Kelly
Комментарии
 0:16:39
0:16:39
 0:08:26
0:08:26
 0:05:59
0:05:59
 0:03:11
0:03:11
 0:00:56
0:00:56
 0:09:46
0:09:46
 0:04:59
0:04:59
 0:01:24
0:01:24
 0:09:37
0:09:37
 0:03:10
0:03:10
 0:00:55
0:00:55
 0:02:49
0:02:49
 0:09:19
0:09:19
 0:14:35
0:14:35
 0:08:09
0:08:09
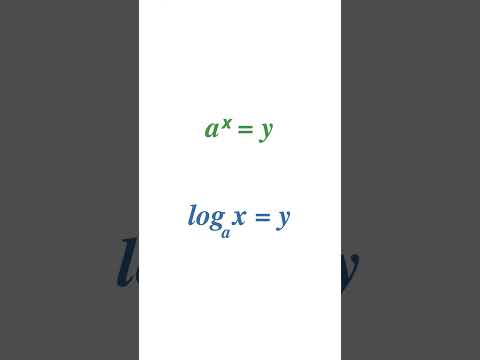 0:00:23
0:00:23
 0:00:28
0:00:28
 0:00:53
0:00:53
 0:25:45
0:25:45
 0:01:55
0:01:55
 0:00:26
0:00:26
 0:01:35
0:01:35
 0:00:51
0:00:51
 0:03:34
0:03:34