filmov
tv
Pythagoras Fibonacci & Pythagorean Series

Показать описание
Today, most western instruments are tuned to a standard “A” of 440 Hz. This standard for tuning has varied over the centuries from the age of Pythagoras to the present. In addition, most popular music that we hear today is played on instruments tuned by equal temperament (an equal gradation of the 12th root of 2 between all notes of the scale). Though some instruments such as pianos and violins can have their temperament changed, fretted instruments such as guitars are usually locked into equal temperament due to the relative placement of their frets.
Having attempted the use of the constant gradient Phi = 1.618..., I discovered that the scale did not resolve to the octave and that the octave contained 13 tones instead of 12. Next, I derived a scale from the Fibonacci series (that converges to a gradation of Phi). Starting with the value 2, I determined the ratios converted to the same octave (from 1.000 to 2.000) by using the lowest values in the Fibonacci sequence. Using the equal-tempered scale as a standard, the remaining tones produced are similar to those of the standard. In the process, I eliminated the value 13 as it produced a micro-tone not close to our familiar equal-tempered notes.
For comparison, I condensed my explanation of the scale derived from the set of Pythagorean ratios from my earlier video notes. This tuning produces a slightly different temperament within each of the twelve keys, unlike the modern equal temperament that is the same for each key. Both tunings are pleasant, though I prefer the one derived from the Pythagorean ratios.
Having attempted the use of the constant gradient Phi = 1.618..., I discovered that the scale did not resolve to the octave and that the octave contained 13 tones instead of 12. Next, I derived a scale from the Fibonacci series (that converges to a gradation of Phi). Starting with the value 2, I determined the ratios converted to the same octave (from 1.000 to 2.000) by using the lowest values in the Fibonacci sequence. Using the equal-tempered scale as a standard, the remaining tones produced are similar to those of the standard. In the process, I eliminated the value 13 as it produced a micro-tone not close to our familiar equal-tempered notes.
For comparison, I condensed my explanation of the scale derived from the set of Pythagorean ratios from my earlier video notes. This tuning produces a slightly different temperament within each of the twelve keys, unlike the modern equal temperament that is the same for each key. Both tunings are pleasant, though I prefer the one derived from the Pythagorean ratios.
 0:02:52
0:02:52
 0:42:35
0:42:35
 0:12:00
0:12:00
 0:03:38
0:03:38
 0:00:57
0:00:57
 0:06:25
0:06:25
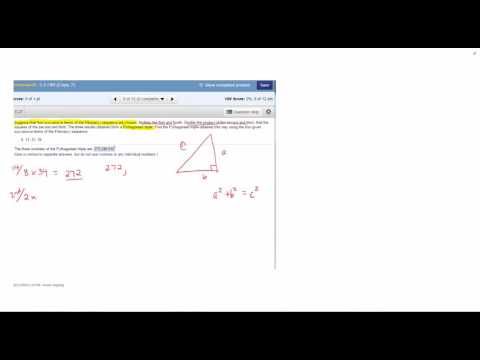 0:03:17
0:03:17
 0:02:40
0:02:40
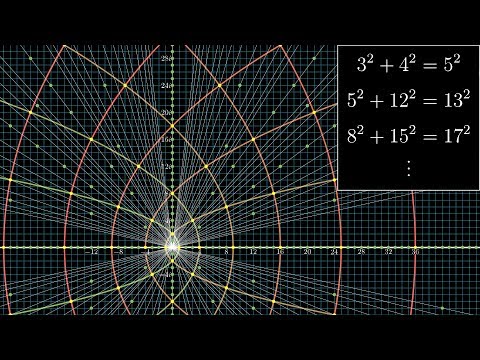 0:16:58
0:16:58
 0:06:43
0:06:43
 0:38:33
0:38:33
 0:04:26
0:04:26
 0:02:42
0:02:42
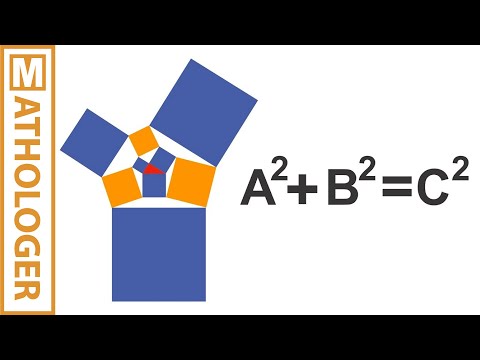 0:21:01
0:21:01
 0:06:10
0:06:10
 2:12:15
2:12:15
 0:01:00
0:01:00
 0:00:34
0:00:34
 0:02:53
0:02:53
 0:19:13
0:19:13
 0:16:51
0:16:51
 0:03:44
0:03:44
 0:20:12
0:20:12
 0:04:50
0:04:50