filmov
tv
Find the limit

Показать описание
In this video, i used the piecewise definition of absolute value to simplify the function, taking one-sided limits was the next important step.
Calculus 1 - Introduction to Limits
How To Find The Limit At Infinity
How to Find Any Limit (NancyPi)
Evaluating Limits By Factoring
3 WAYS TO SOLVE LIMITS
Finding Limits an Algebraic Approach
How To Evaluate Limits From a Graph
Introduction to Limits
FSA Part 4: HOW MUCH CAN YOU CARRYOVER ANNUALLY?
Limits and Continuity
Find the limit
Limits of Trigonometric Functions
Find Limits from Graphs | Calculus 1
Learn how to evaluate a limit at infinity
Infinite Limits and Vertical Asymptotes
Evaluating a limit by factoring
Limits of Rational Functions - Fractions and Square Roots
Solving Limits Mentally #calculus #limit #infinity #rational
Piecewise Functions - Limits and Continuity | Calculus
Find the limit
Limits Calculator Technique
Limits of functions | Calculus
How to Find the Limit at Infinity (NancyPi)
The limit is the limit is the limit is the limit
Комментарии
 0:20:20
0:20:20
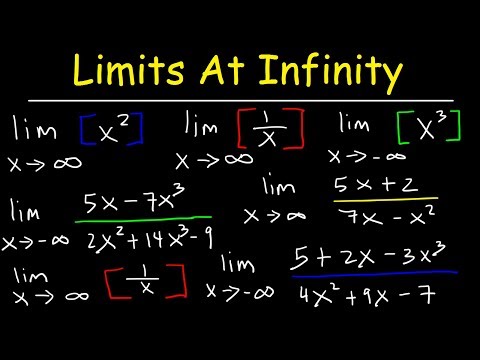 0:13:14
0:13:14
 0:16:42
0:16:42
 0:11:35
0:11:35
 0:05:00
0:05:00
 0:07:41
0:07:41
 0:11:32
0:11:32
 0:11:08
0:11:08
 0:00:43
0:00:43
 0:19:19
0:19:19
 0:06:16
0:06:16
 0:15:23
0:15:23
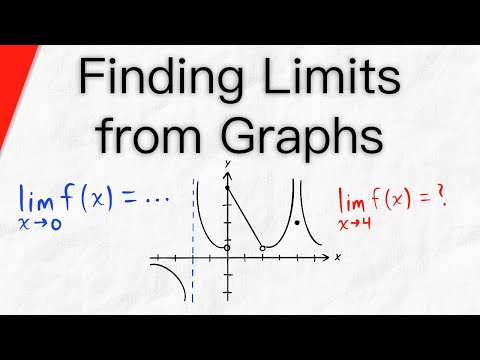 0:11:09
0:11:09
 0:01:40
0:01:40
 0:29:04
0:29:04
 0:04:46
0:04:46
 0:10:06
0:10:06
 0:01:00
0:01:00
 0:10:06
0:10:06
 0:10:11
0:10:11
 0:01:49
0:01:49
 0:15:09
0:15:09
 0:30:49
0:30:49
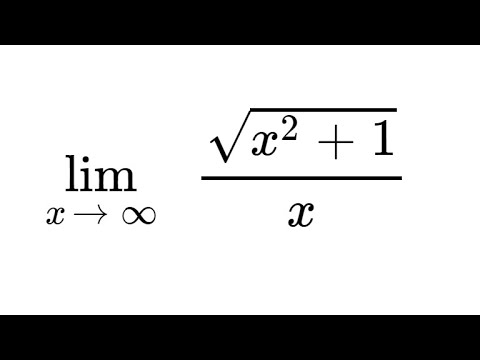 0:00:14
0:00:14