filmov
tv
Physics 32.5 Statistical Thermodynamics (9 of 39) Number of Microstates Analyzed N=10

Показать описание
To donate:
In this video I will analyze the number of microstates when N=10.
Next video in the polar coordinates series can be seen at:
Physics 32.5 Statistical Thermodynamics (9 of 39) Number of Microstates Analyzed N=10
Physics 32.5 Statistical Thermodynamics (5 of 39) The Average Occupation Number
xavier memes #memes
Physics 32.5 Statistical Thermodynamics (24 of 39) N Molecules in a Box: Divided in N Equal Sections
Physics 32.5 Statistical Thermodynamics (11 of 39) Number of Microstates Analyzed N=100
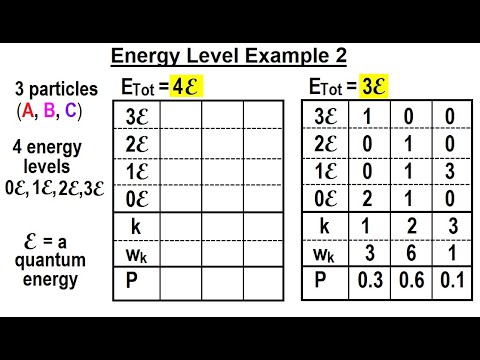
Physics 32.5 Statistical Thermodynamics (33 of 39) Energy Level Example 2
Physics 32.5 Statistical Thermodynamics (34 of 39) Energy Level Example 3
pov: you worked harder for gcses than alevels. #shorts #student
Physics 32.5 Statistical Thermodynamics (7 of 39) Stirling's Approximation Explained
Physics 32.5 Statistical Thermodynamics (31 of 39) General Counting Method for w
How much does a PHYSICS RESEARCHER make?
#pov : my gcse results vs what i predicted #gcse #gcseresults #gcse2022 #results #shortsvideo
How To Solve Math Percentage Word Problem?
Physics 32.5 Statistical Thermodynamics (26 of 39) What is Entropy of 1 mol of Gas Distributed?
Physics 32.5 Statistical Thermodynamics (4 of 39) Understanding Statistical Thermodynamics 2
IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit
Salsa Night in IIT Bombay #shorts #salsa #dance #iit #iitbombay #motivation #trending #viral #jee
11 years later ❤️ @shrads
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
This chapter closes now, for the next one to begin. 🥂✨.#iitbombay #convocation
Thermodynamics (statistical): translational partition function derivation
Physics 32.5 Statistical Thermodynamics (10 of 39) Number of Microstates Analyzed N=50
NEWYES Calculator VS Casio calculator
Comment yes for more body language videos! #selfhelp #personaldevelopment #selfimprovement
Комментарии
 0:07:56
0:07:56
 0:03:20
0:03:20
 0:00:06
0:00:06
 0:04:00
0:04:00
 0:09:06
0:09:06
 0:07:02
0:07:02
 0:08:13
0:08:13
 0:00:10
0:00:10
 0:09:09
0:09:09
 0:07:52
0:07:52
 0:00:44
0:00:44
 0:00:16
0:00:16
 0:00:29
0:00:29
 0:04:57
0:04:57
 0:05:09
0:05:09
 0:00:12
0:00:12
 0:00:14
0:00:14
 0:00:11
0:00:11
 0:00:20
0:00:20
 0:00:16
0:00:16
 0:18:48
0:18:48
 0:07:02
0:07:02
 0:00:14
0:00:14
 0:00:22
0:00:22