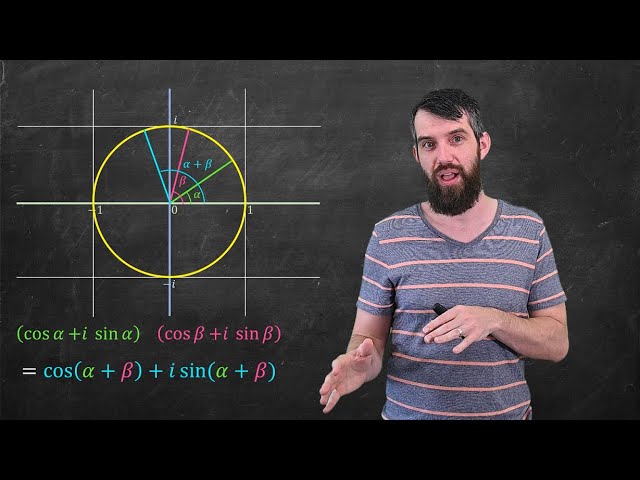
The geometric view of COMPLEX NUMBERS

COURSE PLAYLISTS:

OTHER PLAYLISTS:
► Want to learn math effectively? Check out my "Learning Math" Series:
►Want some cool math? Check out my "Cool Math" Series:

BECOME A MEMBER:

SOCIALS:

[somayazeidan]

I came here just to say that I enjoyed learning with you, you are brilliant and you know how to make us love what we do ❤️

[crimfan]

That's super clear and connects really nicely with the exponential representation because the angles add.

[goalpost]

I just wanna appreciate your effort 💝
Good job Sir.

[itzritam]

love from India. Your videos are really helpful for our engineering and statistical entrance examinations.

[MyMathsAdventure]

Moving onto Argand diagrams, the next chapter after Complex Numbers in my textbook. So great video to plugin any gaps before then 👍🏼

[lavinnasays]

Oh my goodness. This video deserves way may more views. Thank you.

[RubALamp]

Hey. Great video as always. You always deliver. However, have you considered investing in a mic? I don't mean to sound rude of course, but your videos could benefit with better audio quality. Thank you for your content!

[thingintresting]

8:50 no, multiplication by real number also results in Rotation. Check it by taking -1 and every number is a complex number as it can be represented in the Mathematical form of typical complex number.

[johubify]

Great Video! I studied Complex Numbers in maths, and then Vectors in Details in Physics

The resemblance between theme is shocking
What's that about, can anyone explain?

[MikeyBarca]

Short question, I'm a bit rusty with this so this question might sound a bit silly. But on 6:05 we called the horizontal length the cos and the vertical length sin. Now doesn't for example cos(alpha) tell us what the Adjacent side divided by the Hypotenuse equals? And that number is the ratio of the two and not the adjacent side only so why can we call the horizontal line the cos by itself?

[HDitzzDH]

So essentially, graphing complex numbers is the exact same as vectors in linear algebra, just plot each component in their respective axis.

[wakeawake]

Do that trig property stands for more that 2 angle? By the way great video! 👌👌👍👍

[eliasvandenberghe]

God damn, never thought anyone could entertain me with geometry.

[physicslover]

Please also make a video on how to visually evaluate the powers of iota with shortcut and in an instant 💚

[arsenalaman]

Wow its really amazing sir
Thank you sir

[happylife-lulo]

Great video, please can u make a course on number theory and thanks

[zenicv]

I wish someone explained to me like this in 1st year electrical engg. class (noone did and now i understand)

[Anonymous-nzwd]

Great video, but I have a question! why complex Eigen Vectors doesn't have invariant sub-space, according to the definition of Eigen Vectors it must be invariant or in the span but why not for Complex Eigenvalues?

[physicslover]

Wao sir that was amazing . Thanks a lot. The strecting and conpressing concept was awesome . Sir I want to tell you that yesterday I read a topic of triangular inequality from the book of Dennis G Zill. It said that let z and z' be two complex numbers . Then
|z+z'| < & = |z|+|z'|
|z–z'| < & = |z|+|z'|
|z–z'| > & = |z|–|z'|
I think the last one is the most important result. This result must have a nice visualization . I hope if you also make a video in complex numbers playlist on this topic of mods | | . Well I have a good suggestion what if you can somehow download the pdf of FUN WITH TRIGONOMETRY by Vitthal B Jadhav. That book is very colorful and illustrates concepts visually. But unfortunately we can't afford that book. I would be very thankful to you if you either share me the pdf via email or make a video series on trigonometry after reading that book. 💚💚💚

[himanshuchauhan]

I have a doubt, please anybody help me to resolve it, why imaginary axis is is perpendicular to real axis