Example 1.2 || Calculating Total Reluctance || Magnetic Circuit || (Chapman)

(English) Example 1.2
Calculating Total Reluctance || Magnetic Circuit || Example 1.2 (Chapman)

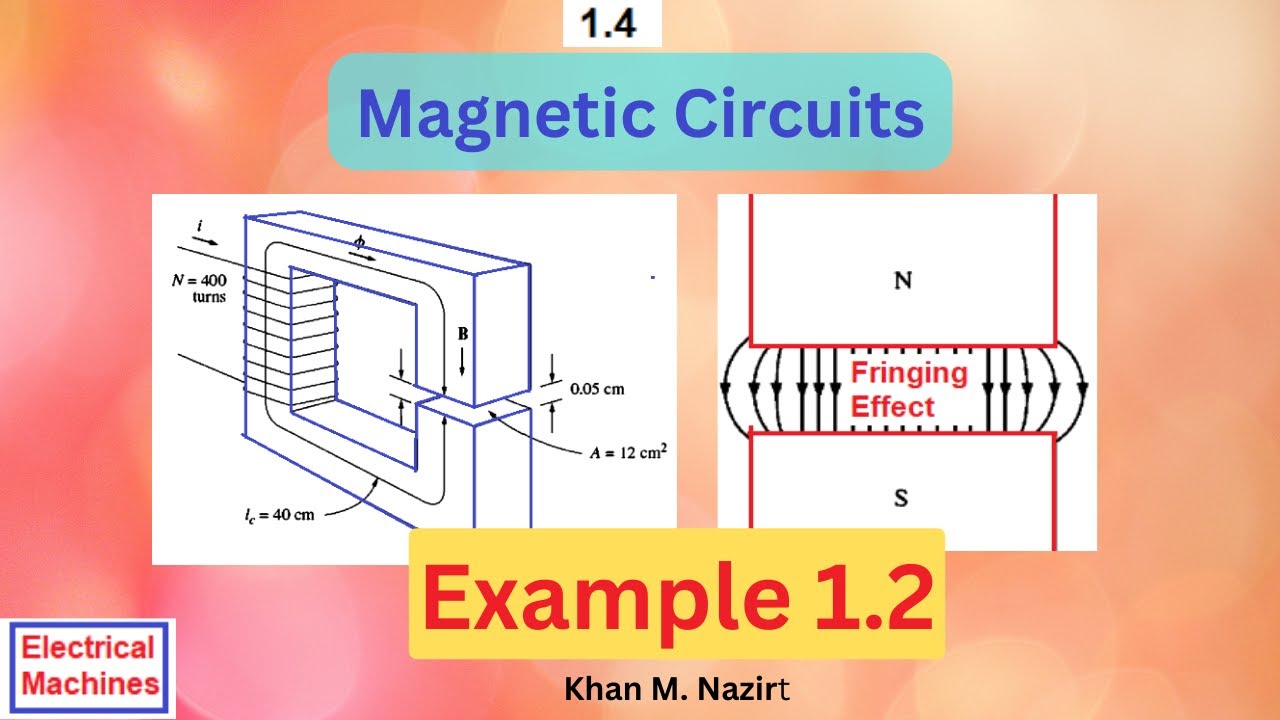
Figure 1- 8a shows a ferromagnetic core whose mean path length is
40 cm. There is a small gap of 0.05 cm in the structure of the otherwise whole core. The cross-sectional area of the core is 12 cm2, the relative permeability of the core is 4000, and the coil of wire on the core has 400 turns.
Assume that fringing in the air gap increases the effective cross-sectional area of the air gap by 5 percent.
Given this information, find
(a) the total reluctance of the flux path (iron plus air gap) and
(b) the current required to produce a flux density of 0.5 T in the air gap.
Beginning:

Mastering Total Reluctance Calculation in Magnetic Circuits - Step by Step Guide!

Understanding Magnetic Circuit Analysis: Example 1.2 (Chapman) Explained!

Demystifying EM 1.4(4)(E): Total Reluctance Calculation Tutorial

Dive into Calculating Total Reluctance: Magnetic Circuit Essentials

The Basics of Magnetic Circuits: Total Reluctance Insights

Middle:

Total Reluctance Calculation: Techniques and Formulas Revealed!

Magnetic Circuit Example 1.2 (Chapman): Analysis and Breakdown!

EM 1.4(4)(E) Simplified: Total Reluctance in Magnetic Circuits

Advanced Techniques for Calculating Total Reluctance

Magnetic Circuits: Understanding Example 1.2 (Chapman)

End:

Mastering Total Reluctance Calculations - Expert Tips and Tricks!

Magnetic Circuit Analysis: Example 1.2 (Chapman) Unveiled

EM 1.4(4)(E): Understanding Total Reluctance in Magnetic Circuits

Unlocking the Secrets of Total Reluctance Calculation

#ElectricalEngineeringAcedemy
Hashtags:
#TotalReluctance #MagneticCircuit #Example1.2 #Chapman #EM1.4(4)(E) #Calculation #Tutorial #Insights #Engineering

SEO Tags:
Total Reluctance Calculation, Magnetic Circuit, Example 1.2, Chapman, EM 1.4(4)(E), Calculation Techniques, Tutorial Insights, Engineering, Magnetic Circuit Analysis, Total Reluctance Formulas, Magnetic Circuit Example, EM Concepts

[malvinmatthew]

For a singly excited elementary two pole reluctance motor under constant current conditions, calculate the maximum torque developed if the rotor radius is equal to 4 cm, the length of the air gap between a pole and the rotor equal to 0.25 cm. the axial length of the rotor equal to 3 cm. The pole excitation is provided by a coil of 1000 turns carrying 5 A.

[surendersingal]

Thank you sir

Great math treaty on reluctance.

[bugrahankutlu]

Sir you're rocking! thx for videos

[rexmagat]

thank you sir... you help me a lot... 1 subscriber here

[ayebazibwebrinton]

thank you so much but on that part of fringing increasing by 5%, does this mean that it can be more than one air gap the fact that you are considering 1+ 5%. thank you

[nawafaljaberi]

for the last questions y did u use the total reluctance and not the air gap reluctance to get the current?

[Hadea_n]

Why did you use the combined reluctance in the final calculation regarding the airgap? I would of thought that only the reluctance of the airgap would be considered?

[fariha-]

Why did we multiply 12cm² with 1.05. I mean where did the value 1.05 come from ?

[Umairshahzad-]

Sir g 1.05 sy multiply kio kya h or agr 5 percent km hoti to kis sy multiply krty

[MaglevYTU]

How do you get A.T/Wb unit for reluctance?

[academicstuff]

why in the second part of question you took area as 12.6 only as it also contains the non fringing part where area is just 12. ???

[shahzamansolangi]

Tomorrow is my paper of electrical machine and i came here to clear my concepts because our teacher didn't teach us well