filmov
tv
Writing a Geometric Series using Sigma / Summation Notation, Ex 2
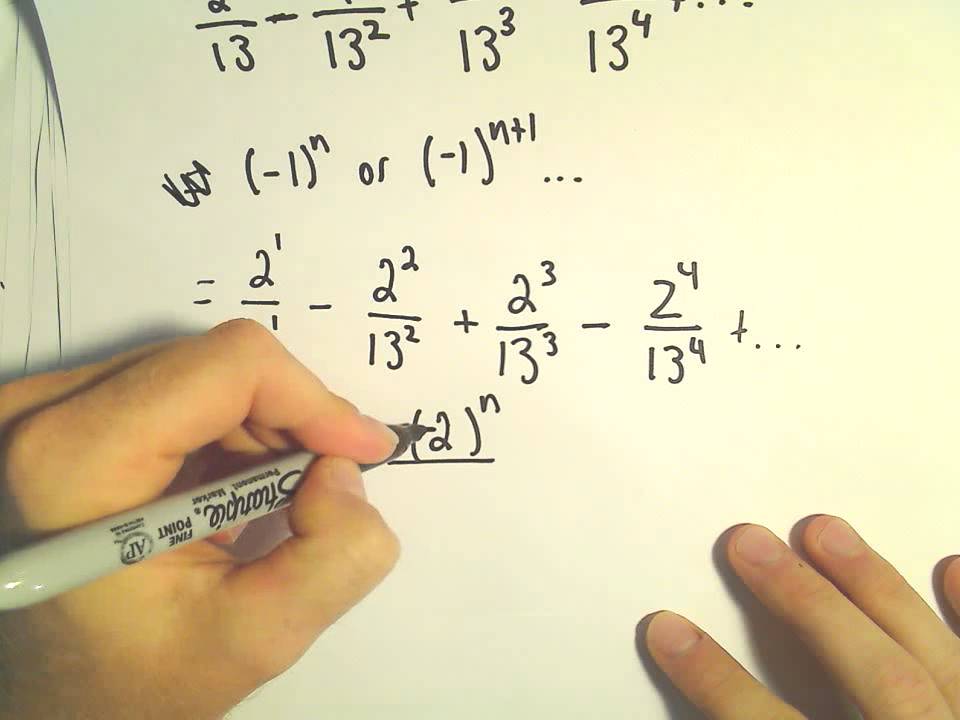
Показать описание
Geometric Series and Geometric Sequences - Basic Introduction
Writing geometric series in sigma notation
Geometric Series | Convergence, Derivation, and Example
Geometric series convergence and divergence examples | Precalculus | Khan Academy
Learn how to write a geometric sequence in summation notation
Writing a Geometric Series using Sigma / Summation Notation
Write a geometric sequence in summation notation
Introduction to geometric sequences | Sequences, series and induction | Precalculus | Khan Academy
Writing a Geometric Series using Sigma / Summation Notation, Ex 2
How to write the sum in sigma notation given a geometric sequence
How To Derive The Sum Formula of a Geometric Series
Explicit & recursive formulas for geometric sequences | High School Math | Khan Academy
Geometric Series | Finding the Sum of Geometric Sequence | Explain in Detailed |
GEOMETRIC PROGRESSION with solved examples
Geometric Sequence Formula
Writing a series in sigma notation
Finding The Sum of an Infinite Geometric Series
Geometric Series Test
Using summation notation to express the sum of a geometric series
Write a Given Finite Geometric Series Using Sigma (Summation) Notation
Writing arithmetic series in sigma notation
10 - Series and Sigma Summation Notation - Part 1 (Geometric Series & Infinite Series)
Sequences and Series (Arithmetic & Geometric) Quick Review
Geometric Sequence: Nth Term and Common Ratio of Geometric Sequence
Комментарии
 0:31:20
0:31:20
 0:03:13
0:03:13
 0:06:28
0:06:28
 0:07:08
0:07:08
 0:01:39
0:01:39
 0:02:12
0:02:12
 0:02:17
0:02:17
 0:10:45
0:10:45
 0:03:07
0:03:07
 0:04:26
0:04:26
 0:14:41
0:14:41
 0:05:37
0:05:37
 0:20:44
0:20:44
 0:08:01
0:08:01
 0:05:48
0:05:48
 0:03:16
0:03:16
 0:19:50
0:19:50
 0:12:24
0:12:24
 0:05:15
0:05:15
 0:05:39
0:05:39
 0:04:07
0:04:07
 0:31:04
0:31:04
 0:19:32
0:19:32
 0:08:23
0:08:23