filmov
tv
Derivative of inverse cosine function from 1st principles
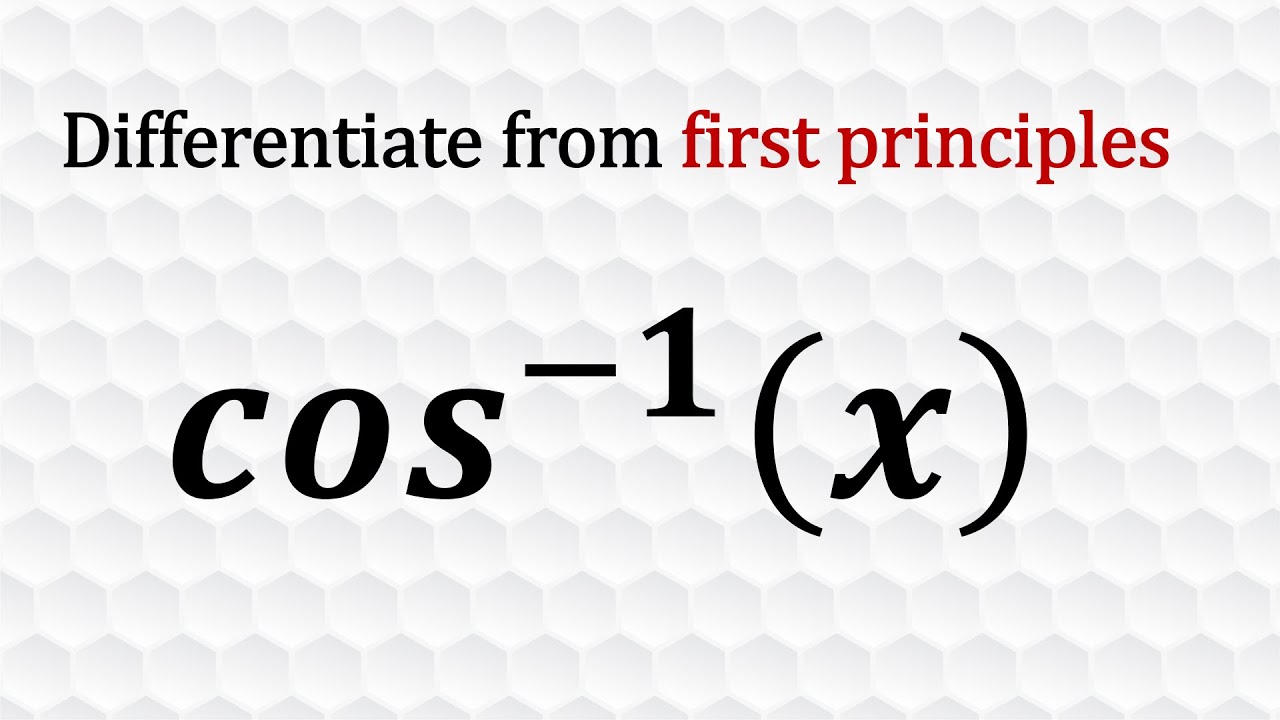
Показать описание
In this video, I showed how to find the derivative of inverse cosine function using the definition of the dereivative
Derivatives of Inverse Trigonometric Functions
Derivative of inverse cosine function
Derivative of inverse cosine function from 1st principles
Inverse trig functions derivatives
Derivatives of Inverse Trigonometric Functions
Prove cos inverse derivation formula Trig Calculus
Derivative of inverse cosine | Taking derivatives | Differential Calculus | Khan Academy
Proof for derivative of sine inverse trig function
Integral of arcsin(x) with Integration by Parts | Calculus 2 Exercises
Differentiation of Inverse trigonometric functions I | Sine inverse, Cosine Inverse and Tan inverse.
The Derivatives of Inverse Trigonometric Functions | Basic Calculus
Calculus 2 Lecture 6.5: Calculus of Inverse Trigonometric Functions
Derivative of inverse sine | Taking derivatives | Differential Calculus | Khan Academy
Calculus - Find the derivative of inverse trigonometric functions
Derivatives of Inverse Trig Functions | Calculus 1 | Math with Professor V
Derivatives of inverse functions | Advanced derivatives | AP Calculus AB | Khan Academy
Derivative Of Inverse Trigonometric Functions
Tricks for Memorizing Inverse Trig Derivatives
Proofs of derivatives of Inverse Trigonometric Functions
Derivatives of inverse trig functions - arcsin (KristaKingMath)
how I remember all the trig and inverse trig derivatives
Derivatives of Inverse Hyperbolic Functions
#Derivative of #inverse #cosine #functions | #trigonometry
Derivatives of Inverse Trigonometric Functions - Calculus 2
Комментарии
 0:06:19
0:06:19
 0:05:30
0:05:30
 0:14:34
0:14:34
 0:13:55
0:13:55
 0:06:21
0:06:21
 0:04:08
0:04:08
 0:03:44
0:03:44
 0:05:31
0:05:31
 0:03:22
0:03:22
 0:16:28
0:16:28
 0:18:35
0:18:35
 1:52:50
1:52:50
 0:04:56
0:04:56
 0:10:13
0:10:13
 0:23:19
0:23:19
 0:04:46
0:04:46
 0:06:00
0:06:00
 0:05:57
0:05:57
 0:06:56
0:06:56
 0:05:06
0:05:06
 0:07:16
0:07:16
 0:12:48
0:12:48
 0:00:16
0:00:16
 0:05:03
0:05:03