filmov
tv
Basis and Dimension of a Vector Space - MathGPT Lesson 8

Показать описание
Hello everyone, in this lesson, we'll be discussing the basis and dimension of a vector space. A basis of a vector space is a set of vectors that, combined, can represent every vector in the space, meaning they are spanning and linearly independent. The number of vectors in a basis is called the dimension of the space.
In this session, we'll concentrate on the crucial concepts of basis and dimension in a vector space. We'll determine whether a given set of vectors forms a basis for a particular vector space and, if so, the dimension of that space.
Let's consider the vector space R², which we've discussed in our previous lessons, and look at the following sets of vectors in R². We'll need to determine several things:
Part A: Are the vectors in the set linearly independent? For our standard basis, the answer is yes.
Part B: Does the set span R²? Again, yes for the standard basis.
Part C: Does the set form a basis for R²? Yes.
Part D: If the set forms a basis for R², what is the dimension of R²? The dimension is two since there are two basis vectors.
Next, let's consider the set S2, which is { (1,1), (1,-1) }. These vectors are not scaled multiples of each other, indicating that they're pointing in unique directions, meaning they're linearly independent and span R². Since the dimension of R² is two, any set that spans R² with only two vectors forms a basis.
However, if a set contains a vector that is a scaled multiple of another, such as in set S3, these vectors are not linearly independent, and they don't span R². Thus, this set doesn't form a basis for R², making the dimensionality question inapplicable.
#Mathematics #LinearAlgebra #VectorSpaces #Basis #Dimension #RealNumbers #MathGPT #LearningMath #MathTutor #MathLesson #MathTutorial #MathReview #StudyMath #MathEducation #MathHelp #UnderstandMath #MathBasics #MathExplained #MathMadeEasy #MathVisualized #AdvancedMathematics
In this session, we'll concentrate on the crucial concepts of basis and dimension in a vector space. We'll determine whether a given set of vectors forms a basis for a particular vector space and, if so, the dimension of that space.
Let's consider the vector space R², which we've discussed in our previous lessons, and look at the following sets of vectors in R². We'll need to determine several things:
Part A: Are the vectors in the set linearly independent? For our standard basis, the answer is yes.
Part B: Does the set span R²? Again, yes for the standard basis.
Part C: Does the set form a basis for R²? Yes.
Part D: If the set forms a basis for R², what is the dimension of R²? The dimension is two since there are two basis vectors.
Next, let's consider the set S2, which is { (1,1), (1,-1) }. These vectors are not scaled multiples of each other, indicating that they're pointing in unique directions, meaning they're linearly independent and span R². Since the dimension of R² is two, any set that spans R² with only two vectors forms a basis.
However, if a set contains a vector that is a scaled multiple of another, such as in set S3, these vectors are not linearly independent, and they don't span R². Thus, this set doesn't form a basis for R², making the dimensionality question inapplicable.
#Mathematics #LinearAlgebra #VectorSpaces #Basis #Dimension #RealNumbers #MathGPT #LearningMath #MathTutor #MathLesson #MathTutorial #MathReview #StudyMath #MathEducation #MathHelp #UnderstandMath #MathBasics #MathExplained #MathMadeEasy #MathVisualized #AdvancedMathematics
 0:10:06
0:10:06
 0:13:20
0:13:20
 0:03:51
0:03:51
 0:08:10
0:08:10
 0:06:20
0:06:20
 0:09:59
0:09:59
 0:10:34
0:10:34
 0:04:02
0:04:02
 8:31:45
8:31:45
 0:03:35
0:03:35
 0:12:45
0:12:45
 0:08:21
0:08:21
 0:04:32
0:04:32
 0:19:00
0:19:00
 0:04:26
0:04:26
 0:04:27
0:04:27
 0:08:00
0:08:00
 0:04:25
0:04:25
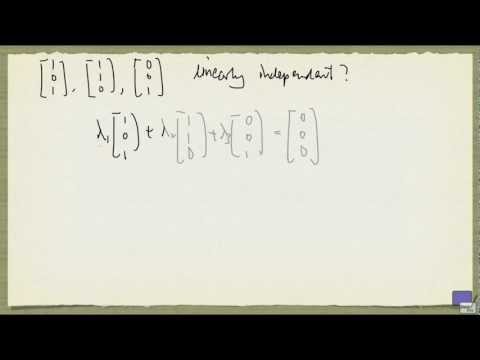 0:12:46
0:12:46
 0:04:22
0:04:22
 0:04:48
0:04:48
 0:05:13
0:05:13
 0:13:32
0:13:32
 0:15:58
0:15:58