Dimension of a Solution Space to a Homogeneous Linear System

preview_player
Показать описание
In this video I demonstrate how to find the basis for the solution space to a homogeneous linear system. The dimension of the solution space is also determined.
  1. Larry Choraszewski "Mr. C"
  2. Dimension
  3. Subspace
  4. Vector Spaces
  5. Basis
  6. Basis Vectors
Рекомендации по теме
Dimension of a 0:08:21

Dimension of a Solution Space to a Homogeneous Linear System

Find the dimension 0:05:05

Find the dimension of solution space of a given matrix A

🔠 Basis Dimension 0:05:47

🔠 Basis Dimension of Solution Space problem ! ! ! ! !

Find Basis and 0:04:26

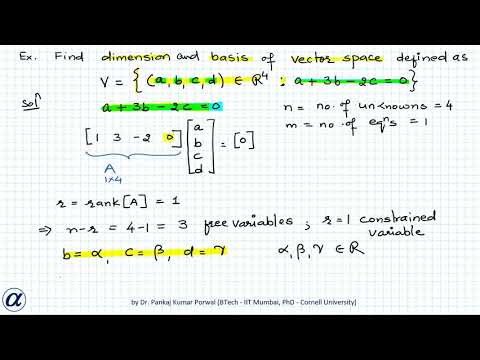
Find Basis and Dimension of Solution Space | Linear Algebra Exercises

Basis and Dimension 0:10:06

Basis and Dimension

Dimension and basis 0:04:21

Dimension and basis for solution space of a homogeneous system of equations Example 1

Dimensions Of Solution 0:14:26

Dimensions Of Solution Space And Vector Space [Linear Algebra] |Formula Foundation Usindh|

Basis and dimension 0:06:20

Basis and dimension

Find a basis 0:04:03

Find a basis and dimension for the solution space of the given homogeneous system

dimension of the 0:03:32

dimension of the solution space | linear algebra in maths

How to find 0:16:17

How to find solution space of the system Ax=0..qu#15 bs I.T 6 SEMESTER

Solution Spaces 0:06:03

Solution Spaces

Basis and dimension 0:38:44

Basis and dimension for solution space Ax=0

Dimension and basis 0:05:16

Dimension and basis for solution space of a homogeneous system of equations Example 2

Dimension and basis 0:06:45

Dimension and basis in Vector Space

Find the rank 0:04:40

Find the rank of the matrix whose dimension and the solution space is given.

Linear Algebra Example 0:09:16

Linear Algebra Example Problems - Matrix Null Space Basis and Dimension

Mathematics: Dimension of 0:01:22

Mathematics: Dimension of solution space (ODE)

dimension of solution 0:02:29

dimension of solution set of differential equation linear algebra

Find Null Space 0:07:53

Find Null Space and Nullity of a Matrix | Linear Algebra

Dimension of Solution 0:15:11

Dimension of Solution space of a homogeneous system AX=0 is n-rank of A- Proof and examples

Basis and Dimension 0:11:02

Basis and Dimension Problem

Dimension of a 0:09:23

Dimension of a Vector Space | Linear Algebra

Solve 2nd Order 0:43:42

Solve 2nd Order DE (Solution Space is 2 Dimensional), Decoupled Systems, Intro to Matrix Exponential

Комментарии
Автор

Thank u bro literally saved me 3 hours before the midterm

spectre
Автор

im not even from your university but you explained it so well in 1/10 of the time that my lecturer took to explain, thank

egemenefe
Автор

Bruh this is so helpful. When you actually try to understand this, its totally easy. Thank you

arturk
Автор

can we say that basis are the solution that satisfies system by writing its parametric equation ? (what i mean basis generates parametrical solution which satisfies the system)

eylmaz
Автор

But how can it even have a basis when it should not be able to form a basis since it fails to be linearly dependent (it forms a nontrivial solution)?

parfittelcano
Автор

Newbie here, why is rref all zeros on Row 2 and 3? shouldn't all rref have diagonal 1's and rest are 0s?

edizon
Автор

How would you do this for a non homogeneous system?

samr
Автор

so in other words you could say that the dimension of a solution space of a system of linear equations (SLE) is definend by n (Number of variables) - rank (of the SLE) = number of free Variables..

davidscherm
Автор

Why do R2 and R3 columns be of zeros in rref?

monicahomwenga