filmov
tv
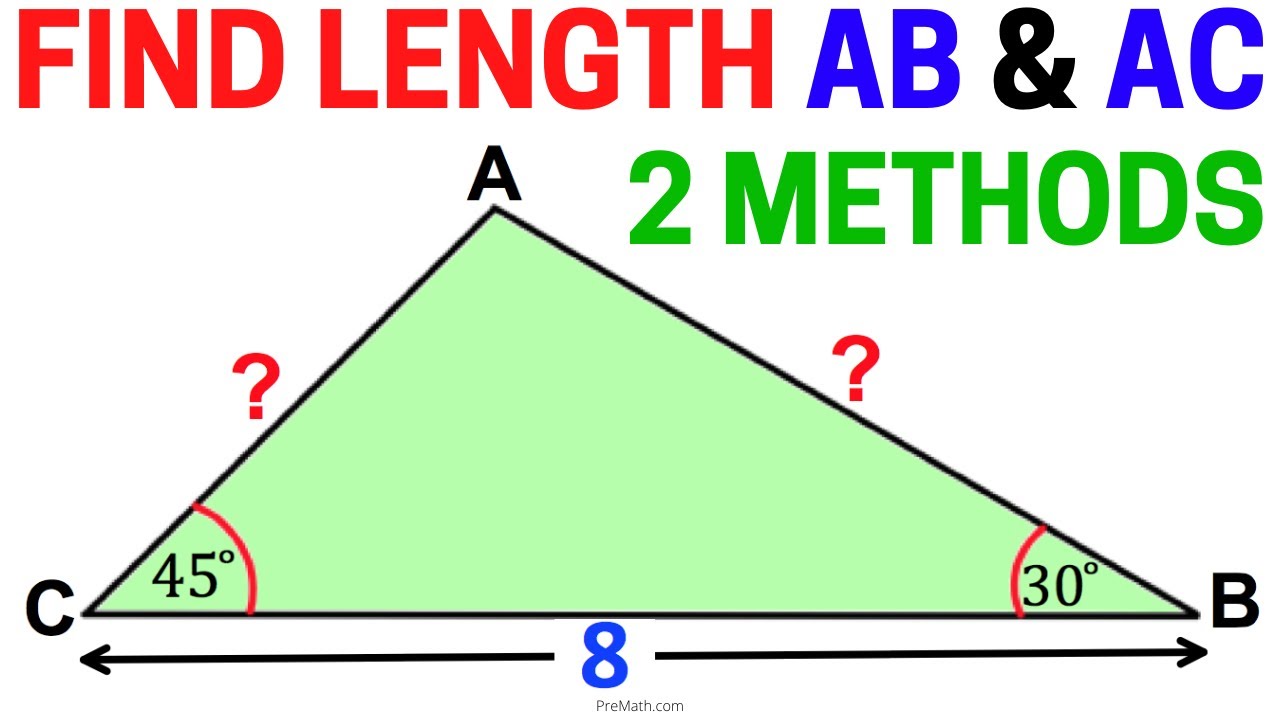
Two Methods: With & Without Trigonometry | Find the Length of AB & AC in this Triangle
Показать описание
Japanese Method #shorts #fyp
Get user location with javascript || Two methods (with/without permission)
Few People Know This Method! How to connect PVC pipes without connectors
Fishing Knots : Two Methods of Tying PR Knot Without Bobbin
Cabling Without a Cable Needle - a Comparison of Two Methods - Cables
How to JOIN YARN the INVISIBLE WAY (2 Methods with No Knots!)
How to Turn OFF Any iPhone Without Buttons (2 Methods)
Boy Kurta cutting without teera ! 2 methods In 1 Video
Have you heard of the OOPS Method? | Rubik's Cube #shorts
How To Release Zip Tie Without Cutting (2 Easy Methods)
Valve stem replace Without tire removal *2 METHODS*
DIY Short Passion Twist | EASY Step-By-Step Tutorial | TWO METHODS (No Crochet & Crochet) | Chev...
Method 2 Is A Hulking Robot Straight Out Of Science Fiction (HBO)
How To Quilt As You Go: My 1 to 3 Method (No Sashing pt 2)
Easy Knotless Box Braid Technique! In 2 hours!! No Feedin method❌
Without formula Method for Beginners | How to Solve a Rubik's Cube 3 x 3 | imw
No Knot Method Tutorial (3 Different Ways)
Stop Receiving WhatsApp Messages without Blocking Someone (2 Methods)
2 Methods Of Cleaning Concrete Without Pressure Washer TESTED.
How To Get Refund On TEMU Without Returning (WORKING) - TEMU NEW METHOD
No Sew Methods: Comparing Stitch Witchery & Fabric Glue
3 methods to get security cameras to work without Wi-Fi | No WiFi Security Camera
How to open a bottle without bottle opener! Quick and easy method!
Cable 2 Front (C2F) without a Cable Needle - Both Methods
Комментарии
 0:00:20
0:00:20
 0:17:46
0:17:46
 0:02:00
0:02:00
 0:10:08
0:10:08
 0:12:50
0:12:50
 0:10:11
0:10:11
 0:01:41
0:01:41
 0:10:44
0:10:44
 0:00:28
0:00:28
 0:01:38
0:01:38
 0:09:13
0:09:13
 0:12:42
0:12:42
 0:03:48
0:03:48
 0:09:27
0:09:27
 0:08:02
0:08:02
 0:22:02
0:22:02
 0:08:03
0:08:03
 0:02:01
0:02:01
 0:08:33
0:08:33
 0:01:40
0:01:40
 0:01:10
0:01:10
 0:06:03
0:06:03
 0:00:21
0:00:21
 0:01:00
0:01:00