filmov
tv
Solving a Radical Inequality
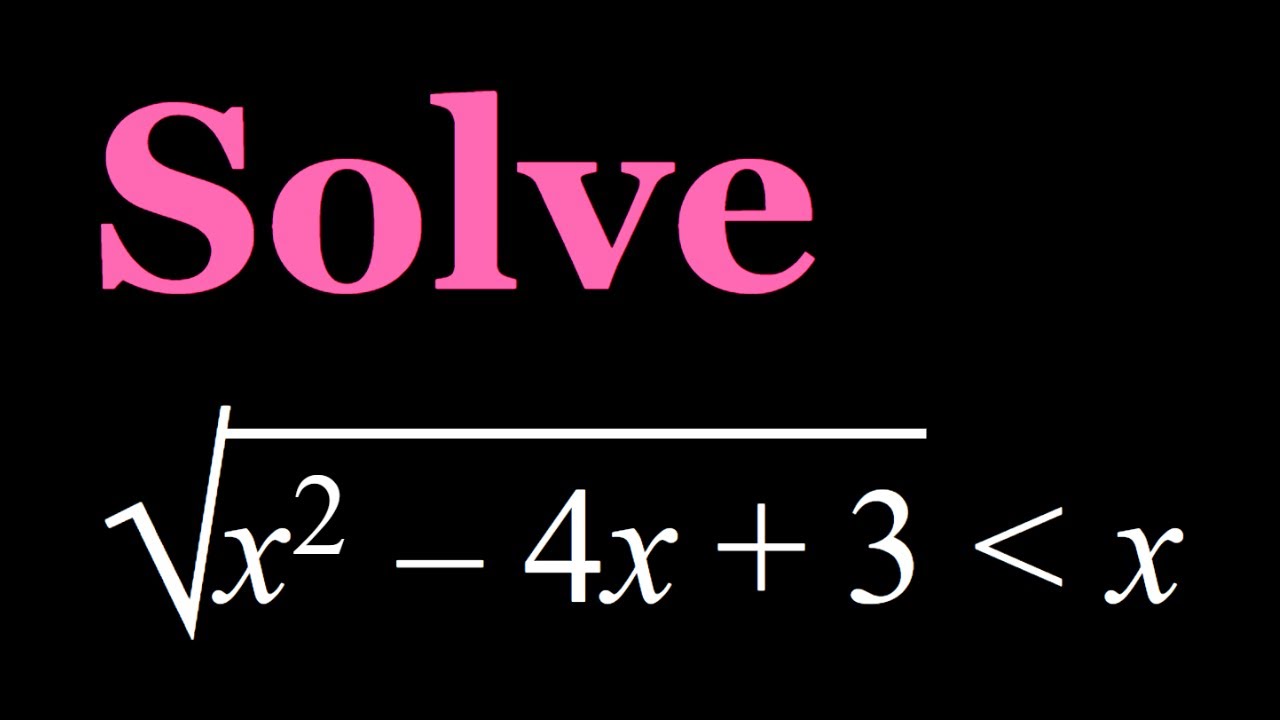
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalInequalities
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #RadicalInequalities
EXPLORE 😎:
PLAYLISTS 🎵 :
Radical Inequalities
Solving a inequality with a square root
Solving a Radical Inequality
Rational Inequalities
Solve a Radical Inequality
Solving Radical Inequality Example
Solving Radical Equations
Solve Square Root Inequality Equations
Pre-Calculus - Solving inequalities with radicals
How to Solve Inequality with Two Square Roots Terms
Solving a Radical Inequality
Why solving a rational inequality is tricky!
Solve a Radical Inequality
How To Solve Linear Inequalities, Basic Introduction, Algebra
Solving Radical Equations With Square Roots, Cube Roots, Two Radicals, Fractions, Rational Exponents
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
Solving an Equation Containing Two Radicals - Example 1
4.4 Solving a Radical Inequality Graphically
Solving Polynomial Inequalities
Solve Radical (Square Root) Equations with Two Radicals
Easy solving the radical inequality. Find x.
Quadratic Inequalities
Solving Radical Inequality Notes
How to Solve & Graph a Rational Inequality with Quadratics in the Numerator & Denominator | ...
Комментарии
 0:03:26
0:03:26
 0:01:12
0:01:12
 0:06:16
0:06:16
 0:10:18
0:10:18
 0:10:53
0:10:53
 0:03:04
0:03:04
 0:17:11
0:17:11
 0:12:51
0:12:51
 0:07:10
0:07:10
 0:12:04
0:12:04
 0:02:27
0:02:27
 0:08:34
0:08:34
 0:06:03
0:06:03
 0:06:24
0:06:24
 0:18:05
0:18:05
 0:03:11
0:03:11
 0:04:37
0:04:37
 0:09:09
0:09:09
 0:12:56
0:12:56
 0:09:31
0:09:31
 0:03:23
0:03:23
 0:12:12
0:12:12
 0:23:21
0:23:21
 0:13:45
0:13:45